题目内容
汽车超速行驶是引发交通事故的主要原因，在社会实践活动期间，高小明和同学尝试用自己所学的知识进行检测公路上行驶的车速，检测方案如下示意图；在距离检测公路100米的观测点P处，观测到一辆小轿车正位于观测点北偏西60°的A处由西向东匀速行驶，经过4秒到达位于观测点北偏西45°的B处．
（1）求A、B之间的距离（精确到0.1米）；
（2）请判断在此时刻，小轿车是否超过了该路段每小时60千米的限制速度？（参考数据：
≈1.414，
≈1.732）
解：（1）在Rt△BOP中，∠BOP=90°，
∵∠BPO=45°，OP=100，
∴OB=OP=100．
在Rt△AOP中，∠AOP=90°，
∵∠APO=60°，
∴AO=OP•tan∠APO．
∴A0=100，
AB=100（-1）（米）；
（2）∵此车的速度=
=25（-1）≈25×0.73=18.25米/秒，
60千米/小时=
≈16.67米/秒，
18.25米/秒＞16.67米/秒，
∴小轿车超过了该路段每小时60千米的限制速度．
分析：（1）分别在Rt△APO，Rt△BOP中，求得AO、BO的长，从而求得AB的长．已知时间则可以根据路程公式求得其速度．
（2）将限速与其速度进行比较，若大于限速则超速，否则没有超速．此时注意单位的换算．
点评：本题考查了解直角三角形的应用，从复杂的实际问题中整理出直角三角形并求解是解决此类题目的关键．
∵∠BPO=45°，OP=100，
∴OB=OP=100．
在Rt△AOP中，∠AOP=90°，
∵∠APO=60°，
∴AO=OP•tan∠APO．
∴A0=100
，AB=100（
-1）（米）；（2）∵此车的速度=
=25（-1）≈25×0.73=18.25米/秒，60千米/小时=
≈16.67米/秒，18.25米/秒＞16.67米/秒，
∴小轿车超过了该路段每小时60千米的限制速度．
分析：（1）分别在Rt△APO，Rt△BOP中，求得AO、BO的长，从而求得AB的长．已知时间则可以根据路程公式求得其速度．
（2）将限速与其速度进行比较，若大于限速则超速，否则没有超速．此时注意单位的换算．
点评：本题考查了解直角三角形的应用，从复杂的实际问题中整理出直角三角形并求解是解决此类题目的关键．
练习册系列答案
相关题目
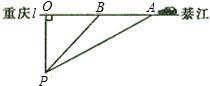据交管部门统计，高速公路超速行驶是引发交通事故的主要原因．我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速，渝黔高速公路某路段的限速是：每小时80千米（即最高时速不超过80千米），如图，他们将观测点设在到公路l的距离为0.1千米的P处．这时，一辆轿车由綦江向重庆匀速直线驶来，测得此车从A处行驶到B处所用的时间为3秒（注：3秒=
（2012•益阳）超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在A处，离益阳大道的距离（AC）为30米．这时，一辆小轿车由西向东匀速行驶，测得此车从B处行驶到C处所用的时间为8秒，∠BAC=75°．
且∠APO=60°，∠BPO=45°． 
（2013•梅列区模拟）汽车超速行驶是引发交通事故的主要原因，在社会实践活动期间，高小明和同学尝试用自己所学的知识进行检测公路上行驶的车速，检测方案如下示意图；在距离检测公路100米的观测点P处，观测到一辆小轿车正位于观测点北偏西60°的A处由西向东匀速行驶，经过4秒到达位于观测点北偏西45°的B处．