Question

【题目】某学校“体育课外活动兴趣小组”，开设了以下体育课外活动项目：A．足球 B．乒乓球C．羽毛球 D．篮球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：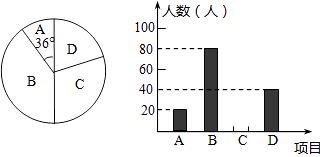

（1）这次被调查的学生共有人，在扇形统计图中“D”对应的圆心角的度数为；
（2）请你将条形统计图补充完整；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加市里组织的乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．

Answer 1

【答案】
（1）200,72°
（2）解：C类人数为200﹣80﹣20﹣40=60（人），

完整条形统计图为：

（3）解：

由上图可知，共有12种等可能的结果，其中恰好选中甲、乙两位同学的结果有2种．

所以P（恰好选中甲、乙两位同学）= =

【解析】解：（1）20÷ =200，

所以这次被调查的学生共有200人，

在扇形统计图中“D”对应的圆心角的度数= ×360°=72°；

所以答案是200，72°；

【考点精析】掌握扇形统计图和条形统计图是解答本题的根本，需要知道能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况；能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况．