题目内容
如图,已知二次函数 的图像过点A(-4,3),B(4,4).
的图像过点A(-4,3),B(4,4).
(1)求二次函数的解析式:
(2)求证:△ACB是直角三角形;
(3)若点P在第二象限,且是抛物线上的一动点,过点P作PH垂直x轴于点H,是否存在以P、H、D、为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由。
 的图像过点A(-4,3),B(4,4).
的图像过点A(-4,3),B(4,4). (1)求二次函数的解析式:
(2)求证:△ACB是直角三角形;
(3)若点P在第二象限,且是抛物线上的一动点,过点P作PH垂直x轴于点H,是否存在以P、H、D、为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由。
解:(1)将A(-4,3),B(4,4)代人 中,
中,
整理得: 解得
解得
∴二次函数的解析式为: ,
,
整理得:
(2)由
整理
∴x1=-2 ,x2=
∴C (-2,0) D
从而有:AC2=4+9 BC2=36+16 AC2+ BC2=13+52=65
AB2=64+1=65
∴ AC2+ BC2=AB2 故△ACB是直角三角形
(3)设 (X<0)
(X<0)
PH= HD=
HD= AC=
AC= BC=
BC=
①当△PHD∽△ACB时有:
即: 整理
整理 
∴
 (舍去)此时,
(舍去)此时,
∴
②当△DHP∽△ACB时有:
即: 整理
整理 
∴
 (舍去)此时,
(舍去)此时,
∴
综上所述,满足条件的点有两个即

 中,
中,整理得:
 解得
解得
∴二次函数的解析式为:
 ,
,整理得:

(2)由

整理

∴x1=-2 ,x2=

∴C (-2,0) D

从而有:AC2=4+9 BC2=36+16 AC2+ BC2=13+52=65
AB2=64+1=65
∴ AC2+ BC2=AB2 故△ACB是直角三角形
(3)设
 (X<0)
(X<0) PH=
 HD=
HD= AC=
AC= BC=
BC=
①当△PHD∽△ACB时有:

即:
 整理
整理 
∴

 (舍去)此时,
(舍去)此时,
∴

②当△DHP∽△ACB时有:

即:
 整理
整理 
∴

 (舍去)此时,
(舍去)此时,
∴

综上所述,满足条件的点有两个即



练习册系列答案
相关题目
 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).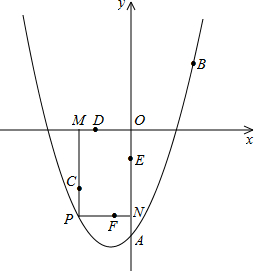 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )