Question

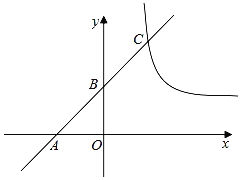
【题目】已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（﹣2，0），与y轴的正半轴交于点B，与反比例函数y＝（x＞0）的图象交于点C，且AB＝BC，点C的纵坐标为4．

（1）求直线AB的表达式；

（2）过点B作BD∥x轴，交反比例函数y＝的图象于点D，求线段CD的长度．

Answer 1

【答案】（1）y＝x+2；（2）2

【解析】

（1）过点C作CH⊥x轴，垂足为H，如图，利用平行线分线段成比例得到＝＝1，则OH＝OA＝2，则点C的坐标为（2，4），然后利用待定系数法求直线AB的解析式；

（2）把C点坐标代入y＝中求出m＝8，再利用直线解析式确定点B的坐标为（0，2），接着利用BD∥x轴得到点D纵坐标为2，根据反比例解析式确定点D坐标，然后根据两点间的距离公式计算CD的长．

解：（1）过点C作CH⊥x轴，垂足为H，如图，

∴＝＝1，

∵A（﹣2，0），

∴AO＝2，

∴OH＝OA＝2，

∵点C的纵坐标为4，

∴点C的坐标为（2，4），

设直线AB的表达式y＝kx+b（k≠0），

把A（﹣2，0），C（2，4）代入得，

解得，

∴直线AB的表达式y＝x+2；

（2）∵反比例函数y＝的图象过点C（2，4），

∴m＝2×4＝8，

∵直线y＝x+2与y轴的正半轴交于点B，

∴点B的坐标为（0，2），

∵BD∥x轴，

∴点D纵坐标为2，

当y＝2时，＝2，解得x＝4，

∴点D坐标为（4，2），

∴CD＝＝2．