题目内容
9.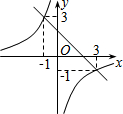 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是x<-1或0<x<3.
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是x<-1或0<x<3.
分析 根据图象知,两个函数的图象的交点是(-1,3),(3,-1).由图象可以直接写出当y1>y2时所对应的x的取值范围.
解答 解:根据图象知,一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$的交点是(-1,3),(3,-1),
故当y1>y2时,x<-1或0<x<3.
故答案为x<-1或0<x<3.
点评 本题主要考查了反比例函数与一次函数的交点问题.解答此题时,采用了“数形结合”的数学思想.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
20.下列几对数中,互为相反数的是( )
| A. | $\frac{3}{4}$和-0.75 | B. | -5和﹢3 | C. | $\frac{1}{3}$和0.3 | D. | $\frac{1}{2}$和-2 |
17.有两根长度分别为5cm和8cm的木棒,若不改变木棒的长度钉成一个三角形木架,则另一根木棒应选( )
| A. | 3cm | B. | 5cm | C. | 13cm | D. | 20cm |
19.已知在1个标准气压下,将1kg水的温度升高℃需要吸收4200J的热量,在同样的条件下,10kg水的温度升高50℃所吸收的热量用科学记数法表示为( )
| A. | 21×105J | B. | 2.1×105J | C. | 2.1×106J | D. | 0.21×107J |
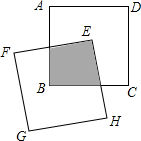 如图,两个边长为1的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E旋转,则它们重叠部分的面积为S=$\frac{1}{4}$.
如图,两个边长为1的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E旋转,则它们重叠部分的面积为S=$\frac{1}{4}$.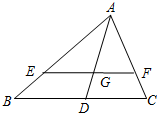 如图,在△ABC中,点G是△ABC的重心,过点G作EF∥BC,交AB于点E,交AC于点F,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{CA}=\overrightarrow b$,用向量$\overrightarrow a$和$\overrightarrow b$表示$\overrightarrow{EF}$.
如图,在△ABC中,点G是△ABC的重心,过点G作EF∥BC,交AB于点E,交AC于点F,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{CA}=\overrightarrow b$,用向量$\overrightarrow a$和$\overrightarrow b$表示$\overrightarrow{EF}$.