题目内容
10. 如图所示,直线y=kx(k<0)与双曲线y=-$\frac{2}{x}$交于M(x1,y1),N(x2,y2)两点,则$\frac{3}{5}$x1y2-3x2y1的值为-$\frac{24}{5}$.
如图所示,直线y=kx(k<0)与双曲线y=-$\frac{2}{x}$交于M(x1,y1),N(x2,y2)两点,则$\frac{3}{5}$x1y2-3x2y1的值为-$\frac{24}{5}$.
分析 由反比例函数图象的特征,得到两交点坐标关于原点对称,故x1=-x2,y1=-y2,再代入$\frac{3}{5}$x1y2-3x2y1,由k=xy得出答案.
解答 解:由图象可知点M(x1,y1),N(x2,y2)关于原点对称,
即-x1=x2,-y1=y2,
把M(x1,y1)代入双曲线y=-$\frac{2}{x}$,得x1y1=-2,
则$\frac{3}{5}$x1y2-3x2y1
=-$\frac{3}{5}$x1y1+3x1y1
=$\frac{6}{5}$-6
=-$\frac{24}{5}$.
故答案为:-$\frac{24}{5}$.
点评 本题考查了正比例函数与反比例函数交点坐标的性质,解决问题的关键是利用两交点坐标关于原点对称.

练习册系列答案
相关题目
1. 已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
 已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )| A. | m>0 | B. | n<0 | C. | mn>0 | D. | m-n<0 |
19.为了解南阳市某小区小孩暑期的学习情况,王老师随机调查了该小区8个小孩某天的学习时间,结果如下(单位:小时):1.5,1.5,2,2.5,3,4,4.5,5,关于这组数据,下列结论错误的是( )
| A. | 众数是1.5 | B. | 中位数是3 | C. | 平均数是3 | D. | 方差是$\frac{13}{8}$ |
19.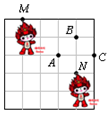 如图,两只福娃发尖所处的位置分别为M(-2,2)、N(1,-1),则A、B、C三个点中为坐标原点的是( )
如图,两只福娃发尖所处的位置分别为M(-2,2)、N(1,-1),则A、B、C三个点中为坐标原点的是( )
 如图,两只福娃发尖所处的位置分别为M(-2,2)、N(1,-1),则A、B、C三个点中为坐标原点的是( )
如图,两只福娃发尖所处的位置分别为M(-2,2)、N(1,-1),则A、B、C三个点中为坐标原点的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 以上都不对 |