题目内容
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E、与OB交于点F,连接CE、CF.
⑴ 求证:AB是⊙O的切线;
⑵ 若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.
圆的直线的关系;三角形全等的求证
解析试题分析:证明:连结OC
∵ OA=OB,C是AB中点, ∴OC⊥AB
又∵点C在⊙O上 ∴AB是⊙O的切线 4分
⑵ 四边形OECF是菱形. 5分
理由:∵ OA=OB,C是AB中点, ∴∠AOC=∠BOC= ∠AOB
∠AOB
又∵OE=OF,OC=OC ∴△OEC≌△OFC
∴CE=CF,∠OCE=∠OCF= ∠ECF
∠ECF
又∵∠AOB=∠ECF ∴∠AOC=∠OCE ∴OE=CE
∴OE=CE=OF=CF
∴四边形OECF是菱形.
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 是直线l,直线AC∥x轴交直线l与点C.
是直线l,直线AC∥x轴交直线l与点C.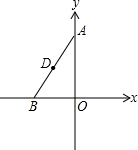 如图,在△ABO中,已知A(0,4),B(-2,0),D为线段AB的中点.
如图,在△ABO中,已知A(0,4),B(-2,0),D为线段AB的中点. (2013•崇左)如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF.
(2013•崇左)如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF. 如图,在△ABO中,AD⊥OB于D,BC⊥OA于C,AD,BC交于点E,且OE平∠AOB,求证:△AEB是等腰三角形.
如图,在△ABO中,AD⊥OB于D,BC⊥OA于C,AD,BC交于点E,且OE平∠AOB,求证:△AEB是等腰三角形.