Question

如图，在△ABC中，∠C=90°，AC+BC=9，点O是斜边AB上一点，以O为圆心2为半径的圆分别与AC、BC相切于点D、E。

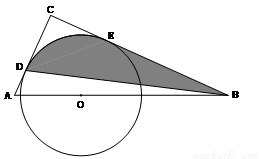
（1）求AC、BC的长；

（2）若AC=3，连接BD，求图中阴影部分的面积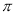（取3.14）。

Answer 1

(1) AC=3，BC=6或AC=6，BC=3；(2)5.14

【解析】

试题分析：（1）连接OD、OE，得出四边形CDOE是正方形，推出CE=CD=OD=OE=2，∠DOE=90°，设AD=x，求出BE=5-x，证△OEB∽△ADO，得出，代入求出x即可；

（2）利用AC=3，AD=3-1=2，BC=6，结合阴影部分的面积S=S△ACB-S△ADB-（S正方形CDOE-S扇形ODE）代入求出即可．

试题解析：（1）连接OD、OE，

∵⊙O切BC于E，切AC于D，∠C=90°，

∴∠ADO=∠BEO=90°，∠ODC=∠C=∠OEC=90°，

∵OE=OD=2，

∴四边形CDOE是正方形，

∴CE=CD=OD=OE=2，∠DOE=90°，

∵∠OEB=∠C=90°，

设AD=x，

∵AC+BC=9，

∴BE=9-2-2-x=5-x，

∴OE∥AC，

∴∠EOB=∠A，

∴△OEB∽△ADO，

∴

∴，

x=1或4，

∴AC=3，BC=6或AC=6，BC=3；

（2）∵AC=3，AD=3-2=1，BC=6，

∴阴影部分的面积S=S△ACB-S△ADB-（S正方形CDOE-S扇形ODE）

=×3×6-×1×6-（2×2-）

=9-3-（4-π）

=2+π

≈5.14．

考点：1.切线的性质；2.扇形面积的计算．