题目内容
如图，OP是∠AOB的平分线，PC⊥OA于点C，PC=2，点D是边OB上一动点，则PD长度最小为________．
2
分析：根据垂线段最短可知，当PD⊥OB时最短，再根据角平分线上的点到角的两边的距离相等可得PD=PC，从而得解．
解答：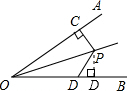
解：∵垂线段最短，
∴当PD⊥OB时PD最短，
∵OP是∠AOB的平分线，PC⊥OA，
∴PD=PC，
∵PC=2，
∴PD=2，
即PD长度最小为2．
故答案为：2．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，垂线段最短的性质，确定出PD最小时的位置是解题的关键．
分析：根据垂线段最短可知，当PD⊥OB时最短，再根据角平分线上的点到角的两边的距离相等可得PD=PC，从而得解．
解答：
解：∵垂线段最短，∴当PD⊥OB时PD最短，
∵OP是∠AOB的平分线，PC⊥OA，
∴PD=PC，
∵PC=2，
∴PD=2，
即PD长度最小为2．
故答案为：2．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，垂线段最短的性质，确定出PD最小时的位置是解题的关键．
练习册系列答案
相关题目
已知如图，OP是∠AOB的平分线，M为OP上一点，E，F是OA上任意两点，C，D是OB上任意两点，且EF=CD，则△FEM与△CDM的面积大小关系为：S△FEM
12、如图，OP是∠AOB的平分线，M是OP上的一点，MC⊥OA，MD⊥OB，若MC=5cm，则MD=
如图，OP是∠AOB的平分线，PC⊥OA于点C，PC=2，点D是边OB上一动点，则PD长度最小为