题目内容
 如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,
如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,
(1)若tan∠BCD= ,AB=10,求CD的长;
,AB=10,求CD的长;
(2)若AB=8,BD=2,设两弓形的面积(图中阴影部分)为S1和S2,求S1-S2.
解:(1)∵∠B+∠CAD=90°,∠B+∠BCD=90°,
∴∠CAD=∠BCD,
∴tan∠CAB=tan∠BCD= ,
,
∴AC=2BC,
∴BC2+(2BC)2=AB2,
∴BC2+(2BC)2=100,
∴BC2=20,
∵BD= CD,
CD,
∴BD2+CD2=BC2,
∴( CD)2+CD2=102,
CD)2+CD2=102,
∴CD=4 .
.
(2)方法一:∵OA=OB,
∴△AOC与△BOC的面积相等,
∴S1-S2=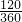 ×π×42-
×π×42- ×π×42=
×π×42= π-
π- π=
π= π;
π;
方法二:S1=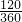 ×π×42-
×π×42- ×4×2
×4×2 =
= π-4
π-4 ,
,
S2= ×π×42-
×π×42- ×4×2
×4×2 =
= π-4
π-4 ,
,
∴S1-S2= π-
π- π=
π= π.
π.
分析:(1)根据等角的三角函数值相等和勾股定理求出BD的长,再根据勾股定理求出CD的长;
(2)根据扇形的面积公式求出S1和S2,再相减即可.
点评:本题考查了扇形面积的计算,根据图形特点,找到公式适用的条件是解题的关键.
∴∠CAD=∠BCD,
∴tan∠CAB=tan∠BCD=
 ,
,∴AC=2BC,
∴BC2+(2BC)2=AB2,
∴BC2+(2BC)2=100,
∴BC2=20,
∵BD=
 CD,
CD,∴BD2+CD2=BC2,
∴(
 CD)2+CD2=102,
CD)2+CD2=102,∴CD=4
 .
.(2)方法一:∵OA=OB,
∴△AOC与△BOC的面积相等,
∴S1-S2=
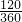 ×π×42-
×π×42- ×π×42=
×π×42= π-
π- π=
π= π;
π;方法二:S1=
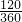 ×π×42-
×π×42- ×4×2
×4×2 =
= π-4
π-4 ,
,S2=
 ×π×42-
×π×42- ×4×2
×4×2 =
= π-4
π-4 ,
,∴S1-S2=
 π-
π- π=
π= π.
π.分析:(1)根据等角的三角函数值相等和勾股定理求出BD的长,再根据勾股定理求出CD的长;
(2)根据扇形的面积公式求出S1和S2,再相减即可.
点评:本题考查了扇形面积的计算,根据图形特点,找到公式适用的条件是解题的关键.

练习册系列答案
相关题目
 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)


