Question

6．如图，在△ABC中，∠BAC=90°，AB=8，AC=6，M为BC上的一动点，ME⊥AB于E，MF⊥AC于F，N为EF的中点，则MN的最小值为（　　）

• A． 4.8
• B． 2.4
• C． 2.5
• D． 2.6

Answer 1

分析 过点A作AM⊥BC于点M′，根据勾股定理求出BC的长，再由三角形的面积公式求出AM′的长．根据题意得出四边形AEMF是矩形，故可得出AM=EF，MN=$\frac{1}{2}$AM，当MN最小时，AM最短，此时M与M′重合，据此可得出结论．

解答 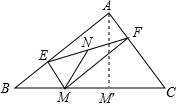解：过点A作AM⊥BC于点M′，
∵在△ABC中，∠BAC=90°，AB=8，AC=6，
∴BC=$\sqrt{{8}^{2}+{6}^{2}}$=10，
∴AM′=$\frac{8×6}{10}$=$\frac{24}{5}$．
∵ME⊥AB于E，MF⊥AC于F，
∴四边形AEMF是矩形，
∴AM=EF，MN=$\frac{1}{2}$AM，
∴当MN最小时，AM最短，此时点M与M′重合，
∴MN=$\frac{1}{2}$AM′=$\frac{12}{5}$=2.4．
故选B．

点评 本题考查了矩形的性质的运用，勾股定理的运用，三角形的面积公式的运用，垂线段最短的性质的运用，解答时求出AM的最小值是关键．