题目内容
下列关于单项式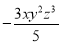 的说法中,正确的是( )
的说法中,正确的是( )
A. 系数是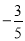 ,次数是5 B. 系数是
,次数是5 B. 系数是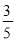 ,次数是5
,次数是5
C. 系数是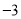 ,次数是6 D. 系数是
,次数是6 D. 系数是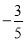 ,次数是6
,次数是6
 D
【解析】∵单项式的系数是,次数是6.
故选D.
D
【解析】∵单项式的系数是,次数是6.
故选D.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下列图形中,右边图形与左边图形成轴对称的是(____)
A. 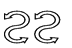
B. 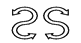
C. 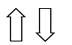
D. 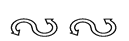
 B
【解析】A、是平移,不符合题意;B、是轴对称,符合题意;C、是旋转,不是轴对称,不符合题意;D、是平移,不符合题意,
故选B.
B
【解析】A、是平移,不符合题意;B、是轴对称,符合题意;C、是旋转,不是轴对称,不符合题意;D、是平移,不符合题意,
故选B. 解方程:(每小题5分,共10分)
(1)2x-3=7x-1 (2)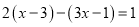 .
.
 (1)x=;(2)x=-6
【解析】试题分析:(1)移项,合并同类项,系数化为1;(2)去括号,移项,合并同类项,系数化为1;
【解析】
(1)2x-3=7x-1,
2x-7x=-1+3,
-5x=2,
x=;
(2),
2x-6-3x+1=1,
2x-3x=1-1+6,
-x=6,
x=-6.
(1)x=;(2)x=-6
【解析】试题分析:(1)移项,合并同类项,系数化为1;(2)去括号,移项,合并同类项,系数化为1;
【解析】
(1)2x-3=7x-1,
2x-7x=-1+3,
-5x=2,
x=;
(2),
2x-6-3x+1=1,
2x-3x=1-1+6,
-x=6,
x=-6. 用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n个“口”字需用棋子枚数为( )

A.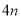 B.
B.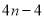 C.
C.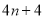 D.
D.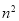
 A
【解析】
试题分析:仔细分析所给图形可得:每个图形中棋子的枚数均为4的倍数,根据这个规律即可求得结果.
由题意得摆第n个“口”字需用棋子枚数为,故选A.
A
【解析】
试题分析:仔细分析所给图形可得:每个图形中棋子的枚数均为4的倍数,根据这个规律即可求得结果.
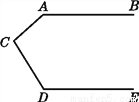
由题意得摆第n个“口”字需用棋子枚数为,故选A. 如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
 证明见解析.
【解析】试题分析:过点C作CF∥AB,结合已知可得∠A+∠ACF=180°,再根据已知角关系可得∠D+∠FCD=180°,根据平行线的判定即可得到CF∥DE,此时再次运用平行线的判定即可解答本题.
试题解析:过点C作CF∥AB.
∵CF∥AB,
∴∠A+∠ACF=180°.
∵∠A+∠ACD+∠D=360°,
∴∠D+∠FCD=180°,
∴...
证明见解析.
【解析】试题分析:过点C作CF∥AB,结合已知可得∠A+∠ACF=180°,再根据已知角关系可得∠D+∠FCD=180°,根据平行线的判定即可得到CF∥DE,此时再次运用平行线的判定即可解答本题.
试题解析:过点C作CF∥AB.
∵CF∥AB,
∴∠A+∠ACF=180°.
∵∠A+∠ACD+∠D=360°,
∴∠D+∠FCD=180°,
∴... 如图,下列说法错误的是( )
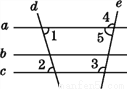
A. 若a∥b,b∥c,则a∥c B. 若∠1=∠2,则a∥c
C. 若∠3=∠2,则b∥c D. 若∠3+∠5=180°,则a∥c
 C
【解析】试题分析:根据平行线的判定进行判断即可.
【解析】
A、若a∥b,b∥c,则a∥c,利用了平行公理,正确;
B、若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;
C、∠3=∠2,不能判断b∥c,错误;
D、若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;
故选C.
C
【解析】试题分析:根据平行线的判定进行判断即可.
【解析】
A、若a∥b,b∥c,则a∥c,利用了平行公理,正确;
B、若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;
C、∠3=∠2,不能判断b∥c,错误;
D、若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;
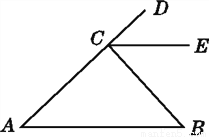
故选C. 如图,∠1和∠2是直线_______和直线________被直线______所截得的同位角;
∠1和∠3是直线_______和直线________被直线______所截得的__________角;
∠2和∠4是直线_______和直线________被直线______所截得的__________角;
∠3和∠4是直线_______和直线________被直线______所截得的__________角;
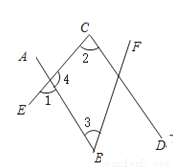
 AB,CD,CE;CE,BF,AB,内错;AB,CD,CE,同旁内;CE,BF,AB,同旁内
【解析】如图,∠1和∠2是直线AB和直线CD被直线CE所截得的同位角;
∠1和∠3是直线CE和直线BF被直线AB所截得的内错角;
∠2和∠4是直线AB和直线CD被直线CE所截得的同旁内角;
∠3和∠4是直线CE和直线BF被直线AB所截得的同旁内角;
AB,CD,CE;CE,BF,AB,内错;AB,CD,CE,同旁内;CE,BF,AB,同旁内
【解析】如图,∠1和∠2是直线AB和直线CD被直线CE所截得的同位角;
∠1和∠3是直线CE和直线BF被直线AB所截得的内错角;
∠2和∠4是直线AB和直线CD被直线CE所截得的同旁内角;
∠3和∠4是直线CE和直线BF被直线AB所截得的同旁内角; 如图,木工师傅在做完门框后,为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的AB,CD两根木条),这样做是运用了三角形的( )
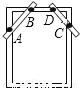
A. 全等性 B. 灵活性 C. 稳定性 D. 对称性
 C
【解析】三角形具有稳定性,其他多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变,故这样做是运用了三角形的稳定性.
故选:C.
C
【解析】三角形具有稳定性,其他多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变,故这样做是运用了三角形的稳定性.
故选:C.