Question

【题目】如图，在四边形 中，，点E为AD边上一点，连接BD、CE，CE与BD交于点F，且CE∥AB，若，则BC的长为__________.

Answer 1

【答案】

【解析】

连接AC交BD于点O，由题意可证AC垂直平分BD，△ABD是等边三角形，可得∠BAO=∠DAO=30°，AB=AD=BD=8，BO=OD=4，通过证明△EDF是等边三角形，可得DE=EF=DF=2，由勾股定理可求OC，BC的长．

如图，连接AC交BD于点O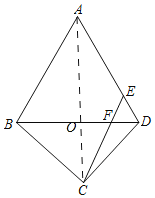

∵AB=AD，BC=DC，∠A=60°，
∴AC垂直平分BD，△ABD是等边三角形
∴∠BAO=∠DAO=30°，AB=AD=BD=8，
BO=OD=4
∵CE∥AB
∴∠BAO=∠ACE=30°，∠CED=∠BAD=60°
∴∠DAO=∠ACE=30°
∴AE=CE=6
∴DE=AD-AE=2
∵∠CED=∠ADB=60°
∴△EDF是等边三角形
∴DE=EF=DF=2
∴CF=CE-EF=4，OF=OD-DF=2
∴OC=,
∴BC=