题目内容
3.已知代数式x2+3x+2,当x=2时,代数式的值可以记作f(2),因此f(2)=22+3×2+2=12,那么当x取任意使代数式有意义的有理数或无理数时,代数式的值都可以记作为f(x),并且将f(x)=x2+3x+2称为f(x)的表达式,这样的表示方法对一切只有一种字母的代数式有效.当出现多个代数式的值时,要用g,h等字母来替代f,从而表示不同代数式的值.试回答下列问题:(1)已知f(x)=9x2+3x+6,求f(2),f(-6);
(2)已知g(g(x))=4x-1,求g(x)的表达式;
(3)已知h(2x+1)=3x2+1,求h(x)的表达式.
分析 (1)根据运算法则,即可解答;
(2)把g(g(x))=4x-1转化为g(g(x))=2(2x-$\frac{1}{3}$)-$\frac{1}{3}$,即可解答;
(3)把h(2x+1)=3x2+1转化为h(2x+1)=$\frac{3}{4}(2x+1)^{2}-\frac{3}{2}$(2x+1)+$\frac{7}{4}$,即可解答.
解答 解:(1)f(2)=9×22+3×2+6=48,f(-6)=9×(-6)2+3×(-6)+6=312.
(2)g(g(x))=2(2x-$\frac{1}{3}$)-$\frac{1}{3}$,
∴g(x)=2x-$\frac{1}{3}$.
(3)∵h(2x+1)=$\frac{3}{4}(2x+1)^{2}-\frac{3}{2}$(2x+1)+$\frac{7}{4}$,
∴h(x)=$\frac{3}{4}{x}^{2}-\frac{3}{2}x+\frac{7}{4}$.
点评 本题考查了代数式求值,解决本题的关键是明确运算法则.

练习册系列答案
相关题目
13. 如图所示的正六棱柱,不是正六棱柱三视图的是( )
如图所示的正六棱柱,不是正六棱柱三视图的是( )
 如图所示的正六棱柱,不是正六棱柱三视图的是( )
如图所示的正六棱柱,不是正六棱柱三视图的是( )| A. |  | B. |  | C. |  | D. |  |
8.下列说法正确的是( )
| A. | 有理数可分为整数、分数和0 | |
| B. | 如果两个数的绝对值相等,那么它们互为相反数 | |
| C. | 边长为a的正方形面积是5,则a是无理数 | |
| D. | 互为相反数的两个数的商是-1 |
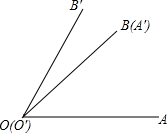 如图,将∠A′O′B′的顶点0′和∠A0B的顶点0重合,边0′A与边0B重合,并使两个角的另一边0A和0′B′分别在重合边0B(O′A)的两旁,这时它们不重合的两边组成∠AOB′.那么∠AOB′,∠A0B与∠A′0′B′之间有什么数量关系?
如图,将∠A′O′B′的顶点0′和∠A0B的顶点0重合,边0′A与边0B重合,并使两个角的另一边0A和0′B′分别在重合边0B(O′A)的两旁,这时它们不重合的两边组成∠AOB′.那么∠AOB′,∠A0B与∠A′0′B′之间有什么数量关系?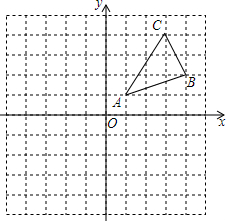 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).