题目内容
 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为
①OH∥BF;②∠CHF=45°;③GH= BC;④FH2=HE•HB.
BC;④FH2=HE•HB.
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:易证Rt△BCE≌Rt△DCF,则∠CBE=∠CDF,利用三角形内角和定理可得到∠EHD=∠BCE=90°,而BE平分∠DBC,根据等腰三角形的性质得到BH平分DF,即HD=HF,易得OH为△DBF的中位线,根据三角形中位线的性质得OH∥BF,则①正确;CH点为Rt△DCF斜边DF上的中线,得到HD=HF=HC,则∠CDH=∠DCH,可得到∠CHF=∠CDF+∠DCH=2×22.5°=45°,②正确;在Rt△DGH中,∠GDH=22.5°,tan∠GDH=tan22.5°= ≠
≠ ,易证得GH≠
,易证得GH≠ BC,则④不正确;易证△HEC∽△HCB,则HC:HB=HE:HC,即HC2=HE•HB,由HC=HF,即可得到④正确.
BC,则④不正确;易证△HEC∽△HCB,则HC:HB=HE:HC,即HC2=HE•HB,由HC=HF,即可得到④正确.
解答:∵四边形ABCD为正方形,
∴CD=CB,
而FC=CE,
∴Rt△BCE≌Rt△DCF,
∴∠CBE=∠CDF,
而∠BEC=∠DEH,
∴∠EHD=∠BCE=90°,即BH⊥DF,
∵BE平分∠DBC,
∴BH平分DF,即HD=HF,
而点O为正方形ABCD的中心,即OD=OB,
∴OH为△DBF的中位线,
∴OH∥BF,则①正确;
∵CH点为Rt△DCF斜边DF上的中线,
∴HD=HF=HC,
∴∠CDH=∠DCH,
而∠CBE=∠CDF= ∠DBC=22.5°,
∠DBC=22.5°,
∴∠CHF=∠CDF+∠DCH=2×22.5°=45°,则②正确;
∵GH∥CF,HD=HF,
∴DG=GC= DC=
DC= BC,
BC,
在Rt△DGH中,∠GDH=22.5°,
tan∠GDH=tan22.5°= ≠
≠ ,
,
∴GH≠ DG,
DG,
∴GH≠ BC,则③不正确;
BC,则③不正确;
∵∠ECH=∠CBH,∠CHE=CHB,
∴△HEC∽△HCB,
∴HC:HB=HE:HC,即HC2=HE•HB,
而HC=HF,
∴HF2=HC•HB,则④正确;
所以正确的结论有三个.
故选C.
点评:本题考查了三角形相似的判定与性质:有两组角对应相等的三角形相似;相似三角形的对应边的比相等.也考查了三角形全等的判定与性质、正方形的性质、直角三角形斜边上的中线性质以及三角形中位线性质.
分析:易证Rt△BCE≌Rt△DCF,则∠CBE=∠CDF,利用三角形内角和定理可得到∠EHD=∠BCE=90°,而BE平分∠DBC,根据等腰三角形的性质得到BH平分DF,即HD=HF,易得OH为△DBF的中位线,根据三角形中位线的性质得OH∥BF,则①正确;CH点为Rt△DCF斜边DF上的中线,得到HD=HF=HC,则∠CDH=∠DCH,可得到∠CHF=∠CDF+∠DCH=2×22.5°=45°,②正确;在Rt△DGH中,∠GDH=22.5°,tan∠GDH=tan22.5°=
 ≠
≠ ,易证得GH≠
,易证得GH≠ BC,则④不正确;易证△HEC∽△HCB,则HC:HB=HE:HC,即HC2=HE•HB,由HC=HF,即可得到④正确.
BC,则④不正确;易证△HEC∽△HCB,则HC:HB=HE:HC,即HC2=HE•HB,由HC=HF,即可得到④正确.解答:∵四边形ABCD为正方形,
∴CD=CB,
而FC=CE,
∴Rt△BCE≌Rt△DCF,
∴∠CBE=∠CDF,
而∠BEC=∠DEH,
∴∠EHD=∠BCE=90°,即BH⊥DF,
∵BE平分∠DBC,
∴BH平分DF,即HD=HF,
而点O为正方形ABCD的中心,即OD=OB,
∴OH为△DBF的中位线,
∴OH∥BF,则①正确;
∵CH点为Rt△DCF斜边DF上的中线,
∴HD=HF=HC,
∴∠CDH=∠DCH,
而∠CBE=∠CDF=
 ∠DBC=22.5°,
∠DBC=22.5°,∴∠CHF=∠CDF+∠DCH=2×22.5°=45°,则②正确;
∵GH∥CF,HD=HF,
∴DG=GC=
 DC=
DC= BC,
BC,在Rt△DGH中,∠GDH=22.5°,
tan∠GDH=tan22.5°=
 ≠
≠ ,
,∴GH≠
 DG,
DG,∴GH≠
 BC,则③不正确;
BC,则③不正确;∵∠ECH=∠CBH,∠CHE=CHB,
∴△HEC∽△HCB,
∴HC:HB=HE:HC,即HC2=HE•HB,
而HC=HF,
∴HF2=HC•HB,则④正确;
所以正确的结论有三个.
故选C.
点评:本题考查了三角形相似的判定与性质:有两组角对应相等的三角形相似;相似三角形的对应边的比相等.也考查了三角形全等的判定与性质、正方形的性质、直角三角形斜边上的中线性质以及三角形中位线性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点F为正方形内一点,在正方形外有一点E,满足∠ABF=∠CBE,BF=BE.
如图,点F为正方形内一点,在正方形外有一点E,满足∠ABF=∠CBE,BF=BE.
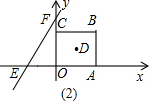

 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论为( )
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论为( )  如图,点F为正方形ABCD的边CD的中点,E为BC上一点,M为EF上一点,且D、M关于AF对称,B、M关于AE对称,∠CFE的平分线交AE的延长线于G,交BC于N,连CG,下列结论:①△AFG为等腰直角三角形;②CG=2
如图,点F为正方形ABCD的边CD的中点,E为BC上一点,M为EF上一点,且D、M关于AF对称,B、M关于AE对称,∠CFE的平分线交AE的延长线于G,交BC于N,连CG,下列结论:①△AFG为等腰直角三角形;②CG=2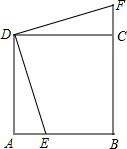 如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.
如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.