题目内容
 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4| 2 |
考点:位似变换,坐标与图形性质
专题:
分析:连接OE、HF,交于点M;易得M是位似中心,又由对角线OE=4\sqrt{2},M是OE的中点,易得答案.
解答: 解:连接OE、HF,交于点M;
解:连接OE、HF,交于点M;
根据题意,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,
易得M是位似中心,故M是OE的中点;
又由对角线OE=4
,
则E的坐标为(-4,4),
M是其中点;
则M的坐标为(-2,2);
故答案是:(-2,2).
 解:连接OE、HF,交于点M;
解:连接OE、HF,交于点M;根据题意,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,
易得M是位似中心,故M是OE的中点;
又由对角线OE=4
| 2 |
则E的坐标为(-4,4),
M是其中点;
则M的坐标为(-2,2);
故答案是:(-2,2).
点评:本题考查了位似中心的确定,对应点的连线或其连线的反向延长线的交点就是位似中心.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(-2,3)与圆M的位置关系是( )
| A、点P在圆内 | B、点P在圆上 |
| C、点P在圆外 | D、不能确定 |
下列运算正确的是( )
| A、2m3+m3=3m6 | ||
| B、m3•m2=m6 | ||
| C、(-m4)3=m7 | ||
D、m6÷2m2=
|
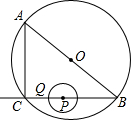 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆,设点Q运动的时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆,设点Q运动的时间为ts.