题目内容
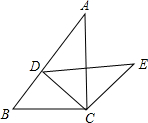 如图所示,△ABC中,AB=5,AC=4,BC=3,点D是AB上的一个动点,∠B=∠EDC,
如图所示,△ABC中,AB=5,AC=4,BC=3,点D是AB上的一个动点,∠B=∠EDC,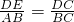 ,设CD=x,△EDC的周长为y,求y与x的函数关系式,并求自变量的取值范围.
,设CD=x,△EDC的周长为y,求y与x的函数关系式,并求自变量的取值范围.
∵∠B=∠EDC,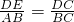
∴△ABC∽△EDC
∵AB=5,AC=4,BC=3,CD=x,
∴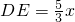 ,
,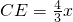 ,
,
∴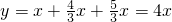 .
.
∵AB=5,AC=4,BC=3,
∴∠C=90°,
∴ ≤CD≤4,即
≤CD≤4,即 ≤x≤4.
≤x≤4.
分析:首先根据边角边定理证得△ABC∽△EDC.根据相似三角形的性质及CD=x,分别用x表示边CE、DE的长.进而求得周长y关于x的函数关系式.根据勾股定理知△ABC为直角三角形,x的最小值即为斜边AB上的高,最大值为AC的长.
点评:本题考查相似三角形的判定与性质、勾股定理、三角形的面积计算.解决本题特别需注意根据相似比,用x表示出边CE、DE的长;勾股定理的几组特殊值3、4、5,12、5、13等常用的数据;
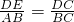
∴△ABC∽△EDC
∵AB=5,AC=4,BC=3,CD=x,
∴
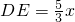 ,
,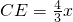 ,
,∴
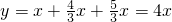 .
.∵AB=5,AC=4,BC=3,
∴∠C=90°,
∴
 ≤CD≤4,即
≤CD≤4,即 ≤x≤4.
≤x≤4.分析:首先根据边角边定理证得△ABC∽△EDC.根据相似三角形的性质及CD=x,分别用x表示边CE、DE的长.进而求得周长y关于x的函数关系式.根据勾股定理知△ABC为直角三角形,x的最小值即为斜边AB上的高,最大值为AC的长.
点评:本题考查相似三角形的判定与性质、勾股定理、三角形的面积计算.解决本题特别需注意根据相似比,用x表示出边CE、DE的长;勾股定理的几组特殊值3、4、5,12、5、13等常用的数据;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
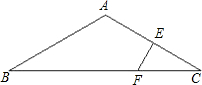 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=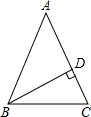 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.