题目内容

如图，A、B是函数数学公式图象上两点，点C、D、E、F分别在坐标轴上，且与点A、B、O构成正方形和长方形．若正方形OCAD的面积为6，则长方形OEBF的面积是


  1. A.
    3
  2. B.
    6
  3. C.
    9
  4. D.
    12
B
分析：根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的四边形的面积S的关系即S=|k|．
解答：∵S正方形OCAD=OD•OC=|xA•yA|=|k|=6，
∴S长方形OCAD=OE•OF=|xB•yB|=|k|=6，
故选B．
点评：本题主要考查反比例函数中比例系数k的几何意义和函数图象的对称性，难易程度适中，是中考较常见的考查点．
练习册系列答案
相关题目
某汽车公司有豪华和普通两种客车在甲、乙两城市之间运营．已知每隔1小时有一辆豪华客车从甲城开往乙城，如图所示，OA是第一辆豪华客车离开甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象，BC是一辆从乙城开往甲城的普通客车距甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象．请根据图中提供的信息，解答下列问题：
（1）点B的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间
 
小时，点B的纵坐标480的意义是
 
．
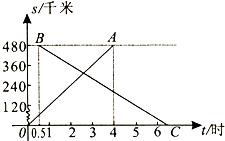（2）请你在原图中直接画出第二辆豪华客车离开甲城的路程s（单位：千米）与运行时间t（单位：精英家教网时）的函数图象．
（3）若普通客车的速度为80千米/时．
①求BC的函数表达式，并写出自变量t的取值范围；
②求第二辆豪华客车出发后多长时间与普通客车相遇；
③直接写出这辆普通客车在行驶途中与迎面而来的相邻两辆豪华客车相遇的间隔时间．
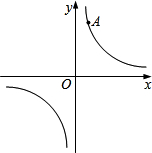精英家教网如图，在直角坐标系中，O为原点．点A在x轴的正半轴上，点B在y轴的正半轴上，tan∠OAB=2．二次函数y=x2+mx+2的图象经过点A，B，顶点为D．
（1）求这个二次函数的解析式；
（2）将△OAB绕点A顺时针旋转90°后，点B落到点C的位置．将上述二次函数图象沿y轴向上或向下平移后经过点C．请直接写出点C的坐标和平移后所得图象的函数解析式；
（3）设（2）中平移后所得二次函数图象与y轴的交点为B1，顶点为D1．点P在平移后的二次函数图象上，且满足△PBB1的面积是△PDD1面积的2倍，求点P的坐标．
精英家教网如图，在直角坐标系中，O为原点．点A在第一象限，它的纵坐标是横坐标的3倍，反比例函数y=
12x
的图象经过点A，
（1）求点A的坐标；
（2）如果经过点A的一次函数图象与直线y=x平行，求这个一次函数的图象与反比例函数图象的另一个交点的坐标．
已知一次函数y=
2
3
x+2的图象分别与坐标轴相交于A，B两点（如图所示），与反比例函数y=
k
x
（k＞0）的图象相交于C点．
（1）作CD⊥x轴，垂足为D，如果OB是△ACD的中位线，求反比例函数y=
k
x
（k＞0）的关系式．
（2）若点P（m，n）在反比例函数图象上，当n＜4时，请结合图象直接写出m取值范围？
某汽车公司有豪华和普通两种客车在甲、乙两城市之间运营．已知每隔1小时有一辆豪华客车从甲城开往乙城，如图所示，OA是第一辆豪华客车离开甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象，BC是一辆从乙城开往甲城的普通客车距甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象．请根据图中提供的信息，解答下列问题：
（1）点B的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间              小时，点B的纵坐标480的意义是                                                 ．
（2）请你在原图中直接画出第二辆豪华客车离开甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象．
（3）若普通客车的速度为80千米/时．
①求BC的函数表达式，并写出自变量t的取值范围；
②求第二辆豪华客车出发后多长时间与普通客车相遇；
③直接写出这辆普通客车在行驶途中与迎面而来的相邻两辆豪华客车相遇的间隔时间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网