题目内容
1. 已知抛物线$y=-\frac{1}{2}{x^2}+2x-1$.
已知抛物线$y=-\frac{1}{2}{x^2}+2x-1$.(1)确定它的开口方向、对称轴和顶点坐标;
(2)在方格图中建立直角坐标系、再列表描点画出它的图象.
分析 (1)先运用配方法,将函数化为顶点坐标式,即y=a(x-h)2+k,再根据二次函数的性质,即可求出开口方向、对称轴和顶点坐标.
(2)由(1)中抛物线的顶点坐标在对称轴的两侧分别取x的值,得出其对应的y的值,描出各点,画出函数图象即可.
解答 解:(1)∵$y=-\frac{1}{2}{x^2}+2x-1$=-$\frac{1}{2}$(x2-4x)-1=-$\frac{1}{2}$(x2-4x+4)-1+2=-$\frac{1}{2}$(x-2)2+1,
∴抛物线开口向下,对称轴是直线x=2,顶点坐标为(2,1).
(2)列表:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{7}{2}$ | -1 | $\frac{1}{2}$ | 1 | $\frac{1}{2}$ | -1 | … |
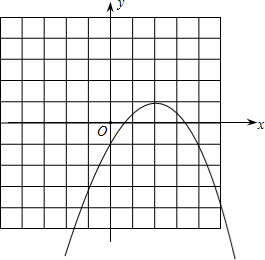
点评 本题考查二次函数的性质,二次函数图象,二次函数图象上点的坐标特征,知道二次函数的顶点坐标公式和画图的方法:列表、描点、连线是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
16.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | x6÷x2=x3 | C. | (-3x3)2=3x6 | D. | x3•x2=x5 |
6.下列一元二次方程中,有两个相等实数根的是( )
| A. | x2-1=0 | B. | x2-x+2=0 | C. | 9x2-6x+1=0 | D. | x2-2x-3=0 |
11.下列计算正确的是( )
| A. | a4•a2=a8 | B. | a+a2=a3 | C. | (a3b)2=a6b2 | D. | -2(x-3y)=-2x-6y |
 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b 的图象经过点B(0,-1),并且与x轴以及y=x+1的图象分别交于点C、D.
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b 的图象经过点B(0,-1),并且与x轴以及y=x+1的图象分别交于点C、D.