题目内容
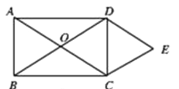
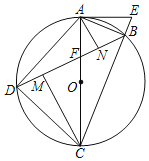
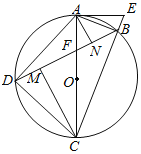
【题目】如图，四边形ABCD内接于⊙O，对角线AC、BD相交于点F，AC是⊙O的直径，延长CB到点E，连接AE，∠BAE＝∠ADB，AN⊥BD，CM⊥BD，垂足分别为点N、M．
（1）证明：AE是⊙O的切线；
（2）试探究DM与BN的数量关系并证明；
（3）若BD＝BC，MN＝2DM，当AE＝
时，求OF的长．
【答案】（1）证明见解析；（2）DM＝BN；证明见解析；（3）OF=
．
【解析】
（1）由圆周角定理得出
，
，得出
，证出
，得出
，即可得出结论；
（2）证
，得出
，证
，得出
，即
，进而得出结论；
（3）由（2）知
，则
，设
，则
，
，
，由勾股定理得出
，证
，得出
，求出
，
，
，由
，求出
，得出
，
，证
，求出
，即可得出答案．
解：（1）证明：
是
的直径，
，
，
，
，
，即
，
，
是的切线；
（2）解：，理由如下：
，
，，
，
，
，
，
，
，
，
，
，即，
，
；
（3）解：由（2）知，则，
设，
，
，
，，，
，
，
是的直径，
，
，
，
，
，
设
，
，
，
，
，即
，
解得：
，
，，
，
，
，
，
，
，
，
，
，
，
，
，
，
．
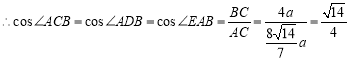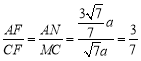练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
