Question

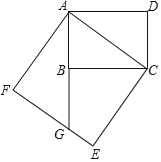
【题目】如图，以矩形ABCD的对角线AC为一边向左下方作正方形ACEF，延长AB交EF于点G，若AB＝3，BC＝4，则EG的长为_____．

Answer 1

【答案】

【解析】

根据勾股定理得到AC=5，根据正方形的性质得到AF=AC=FE=5，∠FAC=90°，根据余角的性质得到∠FAG=∠ACB，根据相似三角形的性质即可得到结论．

解：∵四边形ABCD是矩形，
∴∠ABC=90°，

∵AB=3，BC=4，
∴AC=5，
∵四边形AFEC是正方形，
∴AF=AC=FE=5，∠FAC=90°，
∴∠FAG+∠CAB=∠CAB+∠ACB=90°，
∴∠FAG=∠ACB，
∵∠F=∠ABC=90°，
∴△AFG∽△CBA，
∴
∴
∴FG=
∴GE=FE-FG=，
故答案为：，