Question

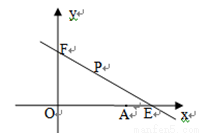
（本题满分12分）如图，直线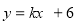与x轴y轴分别相交于点E，F．点E的坐标（8,0）,点A的坐标为（6,0）。点P（x,y）是第一象限内的直线上的一个动点（点P不与点E，F重合）．

（1）求k的值；

（2）在点P运动的过程中，求出△OPA的面积S与x的函数关系式．

（3）若△OPA的面积为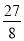，求此时点P的坐标．

Answer 1

（1）；（2）S=；（3）．

【解析】

试题分析：（1）把点E的坐标（8,0）代入可求；（2）过点P作PD⊥OA于点D，△OPA边OA上的高是线段PD，PD的长即点P的纵坐标，因为P（x,y）是上一点，所以PD=,然后根据三角形面积公式计算即可；（3）令S=，求出x的值即可得到点P的坐标．

试题解析：（1）直线与x轴交于点E，且点E的坐标（8,0）

∴，解得

∴

（2）过点P作PD⊥OA于点D，

∵点P（x,y）是第一象限内的直线上的一个动点

∴

而点A的坐标为（6,0）

∴

=

（3）令S=,则=，

解得：x=，代入得y=，

所以点P的坐标是

考点：1．确定一次函数解析式；2．确定点的坐标；3．一次函数的知识综合．