题目内容
 27、如图,在锐角△ABC中,BA=BC,点O是边AB上的一个动点(不与点A、B重合),以O为圆心,OA为半径的圆交边AC于点M,过点M作⊙O的切线MN交BC于点N.
27、如图,在锐角△ABC中,BA=BC,点O是边AB上的一个动点(不与点A、B重合),以O为圆心,OA为半径的圆交边AC于点M,过点M作⊙O的切线MN交BC于点N.(1)当OA=OB时,求证:MN⊥BC;
(2)分别判断OA<OB、OA>OB时,上述结论是否成立,请选择一种情况,说明理由.
分析:(1)连接OM,则OM⊥MN,△OAM中,OA=OM,因此∠A=∠OMA=∠C,因此OM∥BC,故MN⊥BC;
(2)由(1)的证明过程可知:证MN⊥BC,与OA、OB的大小没有关系,因此两种情况都成立.
(2)由(1)的证明过程可知:证MN⊥BC,与OA、OB的大小没有关系,因此两种情况都成立.
解答: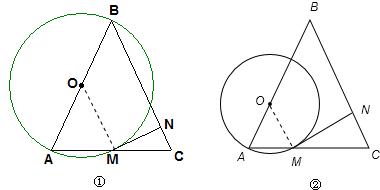 解:(1)证明:连接OM,则OM⊥MN;
解:(1)证明:连接OM,则OM⊥MN;
∵在△OAM中,OA=OM,
∴∠A=∠OMA;
∵在△BAC中,AB=BC,
∴∠A=∠C,
∴∠OMA=∠C,
∴OM∥BC,
∴MN⊥BC;
(2)答:当OA<OB时,成立;当OA>OB时,也成立.
以OA<OB为例进行说明,如图②,OA<OB,连接OM;
∵在△OAM中,OA=OM,
∴∠A=∠OMA;
∵在△BAC中,AB=AC,
∴∠A=∠C,
∴∠OMA=∠C,
∴OM∥BC,
∴MN⊥BC.
 解:(1)证明:连接OM,则OM⊥MN;
解:(1)证明:连接OM,则OM⊥MN;∵在△OAM中,OA=OM,
∴∠A=∠OMA;
∵在△BAC中,AB=BC,
∴∠A=∠C,
∴∠OMA=∠C,
∴OM∥BC,
∴MN⊥BC;
(2)答:当OA<OB时,成立;当OA>OB时,也成立.
以OA<OB为例进行说明,如图②,OA<OB,连接OM;
∵在△OAM中,OA=OM,
∴∠A=∠OMA;
∵在△BAC中,AB=AC,
∴∠A=∠C,
∴∠OMA=∠C,
∴OM∥BC,
∴MN⊥BC.
点评:本题考查了切线的性质、等腰三角形的性质、平行线的判定和性质等知识的综合应用能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
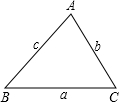 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答: 25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.
25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.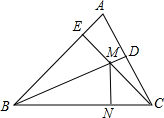 如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=
如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=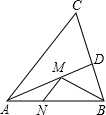 如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是
如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是