题目内容
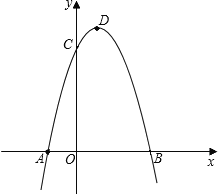
【题目】在平面直角坐标系中，给出如下定义：已知两个函数，如果对于任意的自变量x，这两个函数对应的函数值记为y1、y2，恒有点x,y1和点x,y2关于点x,x成中心对称（此三个点可以重合），由于对称中心x,x都在直线yx上，所以称这两个函数为关于直线yx的“相依函数”.例如：y3x和y5x为关于直线yx的“相依函数”
（1）已知点M1,m是直线y2x4上一点，请求出点M1,m关于点1,1成中心对称的点N的坐标；
（2）若直线y3xn和它关于直线yx的“相依函数”的图象与y轴围成的三角形的面积为8，求n的值；
（3）若二次函数yax2bxc和yx2d为关于直线yx的“相依函数”.
①请求出a、b的值；
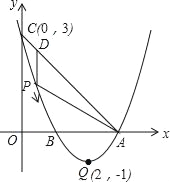
②已知点P3,2、点Q2,2，连接PQ，直接写出yax2bxc和yx2d两条抛物线与线段PQ有且只有两个交点时对应的d的取值范围.
【答案】（1）M (1,6), N (1,4)；（2）n 4；（3）①
，②1 d 2或 7 d 2
【解析】
（1）先把M坐标代入直线y2x4，求出m的值，再根据与点1,1成中心对称即可求出N的坐标;（2）根据相依函数的定义得
，求得依函数解析式为： yxn，联立两函数求出交点的横坐标，再利用y轴围成的三角形的面积为8，得出式子求出n；（3）①由题意得
，即
，恒成立，即可求出a,b的值，②根据题意作出图像，再根据图像进行判断.
解：（1）把M坐标代入直线y2x4，得m=6，
∵M,N关于（1,1）成中心对称，故N（1，-4）
（2）
，可得相依函数解析式为： y x n
；解得：
，解得： n 4
（3）①，可得：，对于任意的 x 要恒成立，
则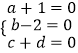
,
②
, 当 3 x 2 的图象如图
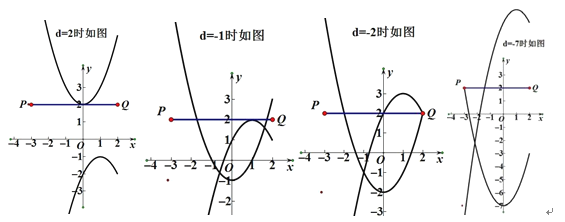
综上图象可知： 1 d 2或 7 d 2
练习册系列答案
相关题目
