题目内容
在梯形ABCD中,AD∥BC,AD=CD,且AC⊥AB,若AB=6,cos∠DBA=
,求AD.
| 9 |
| 11 |
考点:梯形,解直角三角形
专题:几何综合题
分析:作出图形,过点A作AE∥CD交BC于点E,判断出四边形AECD是菱形,根据菱形的性质可得AE=CE=AD,然后求出∠CAE=∠ACE,再根据等角的余角相等求出∠ABC=∠BAE,根据等角对等边可得BE=AE,从而求出AD=AE=
BC,设AC、BD相交于点O,根据cos∠DBA求出OB,利用勾股定理列式求出AO,再根据△AOD和△BOC相似,利用相似三角形对应边成比例列式求出OC,从而得到AC,然后利用勾股定理列式求出BC,即可得解.
| 1 |
| 2 |
解答:解:如图,过点A作AE∥CD交BC于点E,
∵AD∥BC,
∴四边形AECD是平行四边形,
又∵AD=CD,
∴四边形AECD是菱形,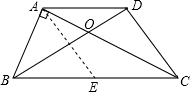
∴AE=CE=AD,
∴∠CAE=∠ACE,
∵AC⊥AB,
∴∠BAE+∠CAE=∠ABC+∠ACE=90°,
∴∠ABC=∠BAE,
∴BE=AE,
∴AD=AE=
BC,
设AC、BD相交于点O,∵AB=6,cos∠DBA=
,
∴OB=6÷
=
,
由勾股定理得,AO=
=
=
,
∵AD∥BC,
∴△AOD∽△BOC,
∴
=
=
,
∴OC=2AO=
,
∴AC=AO+OC=
+
=4
,
在Rt△ABC中,BC=
=
=14,
∴AD=
BC=
×14=7.
∵AD∥BC,
∴四边形AECD是平行四边形,
又∵AD=CD,
∴四边形AECD是菱形,

∴AE=CE=AD,
∴∠CAE=∠ACE,
∵AC⊥AB,
∴∠BAE+∠CAE=∠ABC+∠ACE=90°,
∴∠ABC=∠BAE,
∴BE=AE,
∴AD=AE=
| 1 |
| 2 |
设AC、BD相交于点O,∵AB=6,cos∠DBA=
| 9 |
| 11 |
∴OB=6÷
| 9 |
| 11 |
| 22 |
| 3 |
由勾股定理得,AO=
| OB2-AB2 |
(
|
4
| ||
| 3 |
∵AD∥BC,
∴△AOD∽△BOC,
∴
| AO |
| OC |
| AD |
| BC |
| 1 |
| 2 |
∴OC=2AO=
8
| ||
| 3 |
∴AC=AO+OC=
4
| ||
| 3 |
8
| ||
| 3 |
| 10 |
在Rt△ABC中,BC=
| AB2+AC2 |
62+(4
|
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了梯形的性质,解直角三角形,菱形的判定与性质,相似三角形的判定与性质,勾股定理,难点在于作辅助线构造出菱形和直角三角形并求出AD=
BC.
| 1 |
| 2 |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
若有理数n<-1,则下列式子正确的是( )
A、
| ||
B、-n<
| ||
C、-n2<
| ||
D、-n3<-n2<-n<
|
x2-4x+1=( )
| A、(x-2)2+3 |
| B、(x-2)2-3 |
| C、(x+2)2+3 |
| D、(x+2)2-3 |
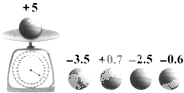 如图,检测5个排球,其中超过标准的克数记为正数,不足的克数记为负数.从轻重的角度看,哪个球最接近标准?( )
如图,检测5个排球,其中超过标准的克数记为正数,不足的克数记为负数.从轻重的角度看,哪个球最接近标准?( )| A、-3.5 | B、+0.7 |
| C、-2.5 | D、-0.6 |

 如图,在四边形ABCD中对角线AC⊥BD,垂足为P,求证:S四边形=
如图,在四边形ABCD中对角线AC⊥BD,垂足为P,求证:S四边形=