题目内容
如图, 在 中,
中,  是
是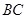 边上的一点,
边上的一点,  是
是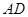 的中点, 过
的中点, 过 点作
点作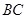 的平行线交
的平行线交 的延长线于点
的延长线于点 , 且
, 且 , 连接
, 连接 .
.
(1) 求证:  是
是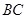 的中点;
的中点;
(2) 若 , 试判断四边形
, 试判断四边形 的形状, 并证明你的结论.
的形状, 并证明你的结论.
(1)通过证明BD=CD,得 是
是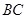 的中点 (2)AFBD是矩形
的中点 (2)AFBD是矩形
解析试题分析:(1)在 中,
中,  是
是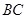 边上的一点,
边上的一点,  是
是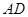 的中点,则AE=DE;过
的中点,则AE=DE;过 点作
点作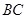 的平行线交
的平行线交 的延长线于点
的延长线于点 , 即AF//CD,得
, 即AF//CD,得 ;又因为
;又因为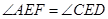 (对顶角相等),所以
(对顶角相等),所以 ,所以AF=CD;
,所以AF=CD; ,所以BD=CD,所以D是BC的中点
,所以BD=CD,所以D是BC的中点
(2)过 点作
点作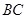 的平行线交
的平行线交 的延长线于点
的延长线于点 , 且
, 且 , 连接
, 连接 .
.
∵AF//BD,AF=BD
∴四边形AFBD是平行四边形,AD=BF,
在 中由(1)的证明知
中由(1)的证明知 是
是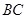 的中点,AF=CD
的中点,AF=CD
∵ ,
,
∴
∴
所以AB=AC;D是BC的中点
所以AD⊥BC,
∴平行四边形AFBD是矩形
考点:三角形全等和矩形
点评:本题考查三角形全等和矩形,解本题的关键是掌握判定三角形全等的方法,会判定一个四边形是否是矩形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 中,
中, 是边
是边 的中点,过点O的直线
的中点,过点O的直线 将
将
 中,
中, 是
是 边的中点,
边的中点, 是
是 的中点,连接
的中点,连接 并延长到点
并延长到点 ,使EF=BE,连结AF、
,使EF=BE,连结AF、 .
. 是矩形,并说明你的理由.
是矩形,并说明你的理由.
 中,
中, 是
是 边的中点,
边的中点, 分别是
分别是 及其延长线上的点,
及其延长线上的点, .
. .
. ,试判断四边形
,试判断四边形 是何种特殊四边形,并说明理由.
是何种特殊四边形,并说明理由.
 中,
中, 是
是 边的中点,
边的中点, 分别是
分别是 及其延长线上的点,
及其延长线上的点, .
. .
. ,试判断四边形
,试判断四边形 是何种特殊四边形,并说明理由.
是何种特殊四边形,并说明理由.