题目内容
下面的四个结论,回答问题.①x2-3x+2=0的两根为x1=1,x2=2;
②(x-1)(x-2)=0的两根为x1=1,x2=2;
③(x-1)(x-2)=x2-3x+2;
④二次三项式x2-3x+2可分解为(x-1)(x-2).
猜测
若关于x的方程x2+px+q=0的两根为x1=3,x2=-4,则二次三项式x2+px+q可分解为
应用在实数范围内分解因式:
(1)2x2-4x+2
(2)
| 1 |
| 3 |
| 2 |
| 3 |
(3)x2-2x-2
分析:猜测:若关于x的方程x2+px+q=0的两根为x1,x2,那么x2+px+q=(x-x1)(x-x2),把所求得的解代入即可;
(1)提取公因式2后用完全平方公式分解即可;
(2)求得方程的相应解为x1,x2,则ax2+px+q=a(x-x1)(x-x2),把所求得的解代入即可;
(3)求得方程的相应解为x1,x2,则x2+px+q=(x-x1)(x-x2),把所求得的解代入即可.
(1)提取公因式2后用完全平方公式分解即可;
(2)求得方程的相应解为x1,x2,则ax2+px+q=a(x-x1)(x-x2),把所求得的解代入即可;
(3)求得方程的相应解为x1,x2,则x2+px+q=(x-x1)(x-x2),把所求得的解代入即可.
解答:解:猜测:(x-3)(x+4)(2分);
应用:(1)原式=2(x2-2x+1)(4分)
=2(x-1)2(5分);
(2)原式=
(x2-2x-3).(7分)
=
(x-3)(x+1)(8分);
(3)设x2-2x-2=0,解这个方程得其解为x=1±
(10分);
∴x2-2x-2=(x-1-
)(x-1+
).(12分)
应用:(1)原式=2(x2-2x+1)(4分)
=2(x-1)2(5分);
(2)原式=
| 1 |
| 3 |
=
| 1 |
| 3 |
(3)设x2-2x-2=0,解这个方程得其解为x=1±
| 3 |
∴x2-2x-2=(x-1-
| 3 |
| 3 |
点评:考查知识点为:若方程ax2+px+q=0的两根为x1,x2,则ax2+px+q=a(x-x1)(x-x2).

练习册系列答案
相关题目

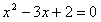 的两根为
的两根为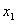 =1,
=1,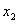 =2;
=2;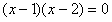 的两根为
的两根为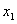 =1,
=1,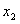 =2;
=2;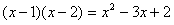 ;
;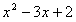 可分解为
可分解为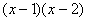 。
。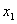 =3,
=3,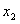 =-4,则二次三项式x2+px+q可分解为________;
=-4,则二次三项式x2+px+q可分解为________; ;②
;②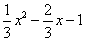 ;③
;③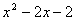 。
。