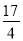��Ŀ����
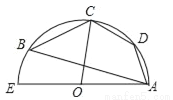
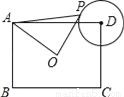
��12�֣���ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ƽ���ı���ABCD�ı�BC��x���ϣ�D����y���ϣ�C������Ϊ��2��0����BC=6����BCD=60�㣬��E��AB��һ�㣬AE=3EB����P��D��O��C���㣬������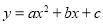 ����D��B��C���㣮
����D��B��C���㣮
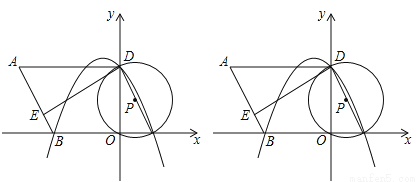
��1���������ߵĽ���ʽ��
��2����֤��ED�ǡ�P�����ߣ�
��3��������ADE�Ƶ�D��ʱ����ת90�㣬E��Ķ�Ӧ��E�������������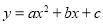 ������˵�����ɣ�
������˵�����ɣ�
��4������MΪ�������ߵĶ��㣬ƽ�����Ƿ���ڵ�N��ʹ���Ե�B��D��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
��1������2��֤���������������3�����ڣ���4��N����5������3������3������ �������� �����������1����ȷ����B�����꣬����Rt��OCD�����á�OCD���������OD�ij����Ӷ��õ���D�����꣬Ȼ�����ý���ʽ�������ߵĽ���ʽ�� ��2���ȼ����CD=2OC=4����ƽ���ı��ε����ʵõ�AB=CD=4��AB��CD����A=��BCD=60�㣬AD=BC=6������AE=3BE�õ�AE=...
��ϰ��ϵ�д�
�����Ŀ
ijЬ��һ���������˶�Ь11˫�����и��ֳ����Ь�����������±���
���루cm�� | 23.5 | 24 | 24.5 | 25 | 25.5 |
��������˫�� | 1 | 2 | 2 | 5 | 1 |
����11˫Ь�ij�����ɵ�һ�������У���������λ���ֱ��ǣ�������
A. 25��25 B. 24.5��25 C. 25��24.5 D. 24.5��24.5
A ��������������������ݱ���ɵ�������25����λ��Ϊ25.

 ��
�� 
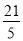 C.
C. 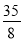 D.
D.