题目内容
 如图,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D=90°,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动,点Q沿BC、CD运动,P点与Q点相遇时停止,设P、Q同时从点B出发x秒时,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x之间的函数关系的大致图象为
如图,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D=90°,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动,点Q沿BC、CD运动,P点与Q点相遇时停止,设P、Q同时从点B出发x秒时,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x之间的函数关系的大致图象为
- A.

- B.

- C.

- D.

C
分析:二次函数开口方向由a的符号确定:当a>0时,开口向上;当a<0时,开口向下.
解答: 解:过点P作PE⊥BC于E,
解:过点P作PE⊥BC于E,
设P、Q同时从点B出发x秒时,△BPQ的面积是y,
∴PE=BP•sin∠B,
∴当点P在AB上,即0<x≤10时,y= BQ•BPsin∠B=
BQ•BPsin∠B= x2×
x2×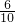 =
= x2;
x2;
∴当点P在AD上,即10≤x≤12时,y=梯形ABCD面积-△PDQ面积=36- PD•QD.而PD=12-x,QD=16-x,则y=-
PD•QD.而PD=12-x,QD=16-x,则y=- x2+14x-60;
x2+14x-60;
P到D之后,面积达到最大36cm2,且不变.
故选C.
点评:二次函数y=ax2+bx+c的图象是一条抛物线,注意掌握各种函数图象的特点.
分析:二次函数开口方向由a的符号确定:当a>0时,开口向上;当a<0时,开口向下.
解答:
 解:过点P作PE⊥BC于E,
解:过点P作PE⊥BC于E,设P、Q同时从点B出发x秒时,△BPQ的面积是y,
∴PE=BP•sin∠B,
∴当点P在AB上,即0<x≤10时,y=
 BQ•BPsin∠B=
BQ•BPsin∠B= x2×
x2×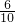 =
= x2;
x2;∴当点P在AD上,即10≤x≤12时,y=梯形ABCD面积-△PDQ面积=36-
 PD•QD.而PD=12-x,QD=16-x,则y=-
PD•QD.而PD=12-x,QD=16-x,则y=- x2+14x-60;
x2+14x-60;P到D之后,面积达到最大36cm2,且不变.
故选C.
点评:二次函数y=ax2+bx+c的图象是一条抛物线,注意掌握各种函数图象的特点.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=