题目内容
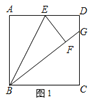
【题目】![]() 如图
如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 边于点
边于点![]() ,则
,则![]() ,求出此时
,求出此时![]() 的值;
的值;
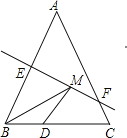
![]() 如图
如图![]() ,矩形
,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,同样将
边的中点,同样将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 边于点
边于点![]() .
.
①证明:![]() ;
;
②若点![]() 恰是
恰是![]() 边的中点,求
边的中点,求![]() 的值;
的值;
③若![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.

【答案】![]()
![]() ;
;![]() ①见解析;②
①见解析;②![]() ,③
,③![]() .
.
【解析】
(1)首先设DG为x,则由正方形的性质即可求得BG与CG的值,利用勾股定理构造方程,解方程即可求得DG的值;
(2)①首先连接EG,由△FBE是由△ABE翻折得到的,利用HL,即可求得Rt△EFG≌Rt△EDG,则可证得DG=FG;
②由G是CD的中点,得到DG与CG的值,在Rt△BCG中,利用勾股定理即可求得AD的长;
③由平行线与翻折变换的性质,易得:∠ABE=![]() ∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.
∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.
![]() 解:设
解:设![]() 为
为![]() ,
,
由题意得:![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
有:![]() ,
,
解得:![]() .
.
∴![]() ;
;![]() ①证明:连接
①证明:连接![]() ,
,
∵![]() 是由
是由![]() 翻折得到的,
翻折得到的,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ;
;
②解:若![]() 是
是![]() 的中点,则
的中点,则![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
③解:由题意![]() ,
,
∴![]() .
.
∵![]() 是由
是由![]() 翻折得到的,
翻折得到的,
∴![]() ,
,
∴![]() .
.
∴若![]() 与
与![]() 相似,则必有
相似,则必有![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目