Question

【题目】以点P为端点竖直向下的一条射线PN，以它为对称轴向左右对称摆动形成了射线PN1，PN2，我们规定：∠N1PN2为点P的“摇摆角”，射线PN摇摆扫过的区域叫作点P的“摇摆区域”（含PN1，PN2）．

在平面直角坐标系xOy中，点P（2，3）．

（1）当点P的摇摆角为60°时，请判断O（0，0）、A（1，2）、B（2，1）、C（2+，0）属于点P的摇摆区域内的点是　 　（填写字母即可）；

（2）如果过点D（1，0），点E（5，0）的线段完全在点P的摇摆区域内，那么点P的摇摆角至少为　 　°；

（3）⊙W的圆心坐标为（a，0），半径为1，如果⊙W上的所有点都在点P的摇摆角为60°时的摇摆区域内，求a的取值范围．

Answer 1

【答案】(1) B、C；（2）90°；（3）2﹣≤a≤2+.

【解析】

（1）根据题意作出图象，从而得到答案；

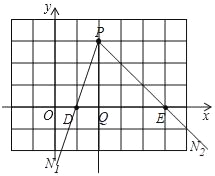
（2）如图所示，当射线PN1过点D时，由对称性可知，此时点E不在点P的摇摆区域内，

当射线PN2过点E时，由对称性可知，此时点D在点P的摇摆区域内，易知：此时PQ＝QE，从而得到∠EPQ的度数，从而得到答案；

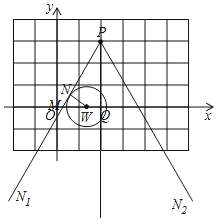
（3）设直线PN1与x轴交于点M，⊙W与射线PN1相切于点N，P为端点竖直向下的一条射线PN与x轴交于点Q，由题意可知：∠PMW＝60°，利用三角函数求出MW，MQ的值，从而得到OM，OW的值，得到两个W的坐标，从而得到a的取值范围.

解：（1）根据“摇摆角”作出图形，如图所示，

将O、A、B、C四点在平面直角坐标系中描出，后，

可以发现，B、C在点P的摇摆区域内，

故属于点P的摇摆区域内的点是B、C

（2）如图所示，当射线PN1过点D时，

由对称性可知，此时点E不在点P的摇摆区域内，

当射线PN2过点E时，

由对称性可知，此时点D在点P的摇摆区域内，

易知：此时PQ=QE，

∴∠EPQ=45°，

∴如果过点D（1，0），点E（5，0）的线段完全在点P的摇摆区域内，那么点P的摇摆角至少为90°

（3）如果⊙W上的所有点都在点P的摇摆角为60°时的摇摆区域内，

此时⊙W与射线PN1相切，

设直线PN1与x轴交于点M，⊙W与射线PN1相切于点N，P为端点竖直向下的一条射线PN与x轴交于点Q，

由定义可知：∠PMW=60°，

∵NW=1，PQ=3，

∴sin∠PMW=，tan∠PMW=

∴MW=，MQ=，

∴OM=2﹣，

∴OW=OM+MW=2﹣+=2﹣

∴此时W的坐标为：（2﹣，0）

由对称性可知：当⊙W与射线PN2相切时，

此时W的坐标为：（2+，0）

∴a的范围为：2﹣≤a≤2+