题目内容
13. 如图,⊙O的弦AB垂直于直径CD于点E,∠BCE=22.5°,AB=2,则⊙O的半径长为( )
如图,⊙O的弦AB垂直于直径CD于点E,∠BCE=22.5°,AB=2,则⊙O的半径长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
分析 连接OB,利用垂径定理求得BE的长,然后求得∠OBE的度数,证明△OBE是等腰直角三角形,据此即可求解.
解答  解:连接OB.
解:连接OB.
∵AB⊥CD,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$×2=1.
在直角△BCE中,∠B=90°-∠BCE=90°-22.5°=67.5°,
∵OC=OB,
∴∠CBO=∠BCE=22.5°,
∴∠OBE=67.5°-22.5°=45°,
∴△OBE是等腰直角三角形,
∴OB=$\sqrt{2}$BE=$\sqrt{2}$.
故选A.
点评 本题考查了垂径定理和等腰直角三角形的性质,正确求得∠OBE的度数是关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
4. 如图是变量y与x之间的函数图象,则函数y的取值范围是( )
如图是变量y与x之间的函数图象,则函数y的取值范围是( )
 如图是变量y与x之间的函数图象,则函数y的取值范围是( )
如图是变量y与x之间的函数图象,则函数y的取值范围是( )| A. | -3≤y≤3 | B. | 0≤y≤2 | C. | 0≤y≤3 | D. | 1≤y≤3 |
8.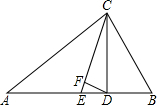 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
5.已知在Rt△ABC中,∠C=90°,AC=2,BC=3,则AB的长为( )
| A. | 4 | B. | $\sqrt{5}$ | C. | $\sqrt{13}$ | D. | 5 |
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,3),B(3,1),C(5,4).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,3),B(3,1),C(5,4). 如图所示,几何体是由4个相同的正方体组成的,它的左视图是( )
如图所示,几何体是由4个相同的正方体组成的,它的左视图是( )


