Question

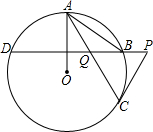如图，已知⊙O的两条弦AC、BD相交于点Q，OA⊥BD．
（1）求证：AB²=AQ•AC；
（2）若过点C的⊙O的切线交DB的延长线于点P，求证：PC=PQ．

Answer 1

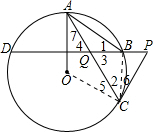证明：（1）连接BC，
∵OA⊥BD，
∴=．
在△ABQ与△ACB中，
∵∠BAQ=∠CAB，
∵=，
∴∠ABD=∠ACB．
∴△ABQ∽△ACB．
∴=．
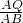∴AB²=AQ•AC．

（2）连接OC，
∵OA=OC，
∴∠ACO=∠CAO．
又∵PC是⊙O的切线，
∴OC⊥PC．
∴∠2+∠5=90°．
∵OA⊥DB，
∴∠4+∠7=90°．
∵OA=OC∠3=∠4，
∴∠5=∠7．
∴∠2=∠3．
∴PC=PQ．
分析：（1）要求证AB²=AQ•AC，可以转化为△ABQ∽△ACB．
（2）要求证PC=PQ，可以根据等角对等边可以证得．
点评：证明线段的乘积相等的问题可以转化为证明三角形相似．可以利用等角对等边证明了线段相等．