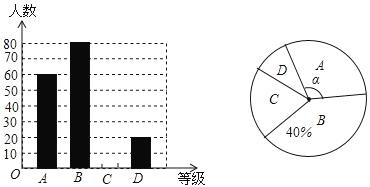
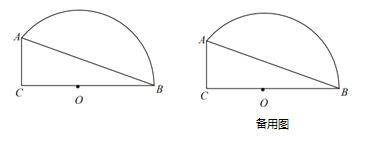题目内容
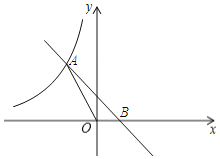
【题目】如图,一条直线与反比例函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() 轴,垂足为
轴,垂足为![]() .
.
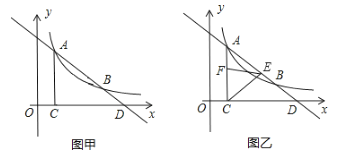
(1)如图甲,求反比例函数的解析式与![]() 点的坐标;
点的坐标;
(2)如图乙,若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,作
,作![]() ,
,![]() 交
交![]() 于
于![]() 点.试说明
点.试说明![]() .
.
【答案】(1)y=![]() ,D点坐标为(5,0); (2)证明见解析.
,D点坐标为(5,0); (2)证明见解析.
【解析】
(1)根据点A的坐标即可求出反比例函数的解析式;再求出B点的坐标B(4,1),即得n=1;利用待定系数法求一次函数的解析式,令一次函数的y=0,求得点D的坐标D(5,0);
(2)要证△CDE∽△EAF,只要证明出△CDE和△EAF的三个内角分别对应相等,即可得证;
解:(1)∵点A(1,4)在反比例函数图象上
∴k=4
即反比例函数关系式为![]() ;
;
②∵点B(4,n)在反比例函数图象上
∴n=1
设一次函数的解析式为y=mx+b
∵点A(1,4)和B(4,1)在一次函数y=mx+b的图象上
∴![]() ,
,
解得![]() ,
,
∴一次函数关系式为y=﹣x+5
令y=0,得x=5
∴D点坐标为(5,0);
(2)证明:∵A(1,4),D(5,0),AC⊥x轴
∴C(1,0)
∴AC=CD=4,
即∠ADC=∠CAD=45°,
∵∠AEC=∠ECD+∠ADC=∠ECD+45°,
∠AEC=∠AEF+∠FEC=∠AEF+45°,
∴∠ECD=∠AEF,
∴△CDE∽△EAF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目