题目内容
 如图,已知A(-3,0),B(0,-4),P为双曲线
如图,已知A(-3,0),B(0,-4),P为双曲线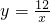 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为
- A.22
- B.23
- C.24
- D.26
C
分析:此题可设P点坐标为(x, ),将四边形分割为四个三角形,四边形ABCD面积的最小,即S△AOB+S△AOD+S△DOC+S△BOC最小.
),将四边形分割为四个三角形,四边形ABCD面积的最小,即S△AOB+S△AOD+S△DOC+S△BOC最小.
解答:设P点坐标为(x, ),x>0,
),x>0,
则S△AOD= ×|-3|×|
×|-3|×| |=
|=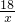 ,S△DOC=
,S△DOC=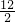 =6,
=6,
S△BOC= ×|-4|×|x|=2x,S△AOB=
×|-4|×|x|=2x,S△AOB= ×3×4=6.
×3×4=6.
∴S△AOB+S△AOD+S△DOC+S△BOC
=12+2x+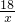
=12+2(x+ )≥12+2×2×
)≥12+2×2×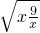 =24.
=24.
故选C.
点评:本题借用考查四边形面积的最小值来考查反比例函数图象的应用,综合能力较强.
分析:此题可设P点坐标为(x,
 ),将四边形分割为四个三角形,四边形ABCD面积的最小,即S△AOB+S△AOD+S△DOC+S△BOC最小.
),将四边形分割为四个三角形,四边形ABCD面积的最小,即S△AOB+S△AOD+S△DOC+S△BOC最小.解答:设P点坐标为(x,
 ),x>0,
),x>0,则S△AOD=
 ×|-3|×|
×|-3|×| |=
|=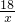 ,S△DOC=
,S△DOC=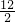 =6,
=6,S△BOC=
 ×|-4|×|x|=2x,S△AOB=
×|-4|×|x|=2x,S△AOB= ×3×4=6.
×3×4=6.∴S△AOB+S△AOD+S△DOC+S△BOC
=12+2x+
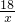
=12+2(x+
 )≥12+2×2×
)≥12+2×2×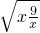 =24.
=24.故选C.
点评:本题借用考查四边形面积的最小值来考查反比例函数图象的应用,综合能力较强.

练习册系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=