题目内容
已知两条直线y=2-x和y=2x+5
(1)试求两条直线的交点坐标;
(2)探求:两条直线与x轴围成的三角形的面积.
解:(1)设两条直线l1和l2的交点坐标为P(x,y),
依题意得: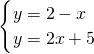
解得: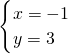
∴P(-1,3).
(2),设两条直线和与x轴的交点为A,B
则A(2,0),B(- ,0),
,0),
∴S△PAB= ×[2-(-
×[2-(- )]×3=
)]×3= .
.
分析:(1)要求两条直线的交点坐标把他们解析式组成方程组解之即可得到交点坐标;
(2)如图,设两条直线和与x轴的交点为A,B,则容易求出A(8,0),B(,0),然后根据已知坐标即可求出两条直线l1和l2与x轴围成的三角形的面积.
点评:此题主要考查平面直角坐标系中交点坐标和图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.
依题意得:
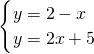
解得:
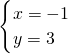
∴P(-1,3).
(2),设两条直线和与x轴的交点为A,B
则A(2,0),B(-
 ,0),
,0),∴S△PAB=
 ×[2-(-
×[2-(- )]×3=
)]×3= .
.分析:(1)要求两条直线的交点坐标把他们解析式组成方程组解之即可得到交点坐标;
(2)如图,设两条直线和与x轴的交点为A,B,则容易求出A(8,0),B(,0),然后根据已知坐标即可求出两条直线l1和l2与x轴围成的三角形的面积.
点评:此题主要考查平面直角坐标系中交点坐标和图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,已知两条直线a,b被第三条直线c所截,若∠1=∠2,求证:∠1=∠3,∠1+∠4=180°.
如图,已知两条直线a,b被第三条直线c所截,若∠1=∠2,求证:∠1=∠3,∠1+∠4=180°. 已知两条直线y1=2x-4和y2=5-x.
已知两条直线y1=2x-4和y2=5-x. 已知两条直线y=(
已知两条直线y=( 如图,已知两条直线AB,CD相交于点O,且CO=DO,AC∥BD,求证:△AOC≌△BOD.
如图,已知两条直线AB,CD相交于点O,且CO=DO,AC∥BD,求证:△AOC≌△BOD.