题目内容
已知⊙O的直径AB、CD互相垂直，弦AE交CD于F，若⊙O的半径为R，求证：AE•AF=2R2．
【答案】分析：连接BE，得到∠AEB=90°，证Rt△AOF∽Rt△AEB即可．
解答：
证明：连接BE，如图，
∵AB为⊙O的直径
∴∠AEB=90°
∵AB⊥CD
∴∠AOF=90°
∴∠AOF=∠AEB=90°
又∠A=∠A
∴△AOF∽△AEB
∴AE•AF=AO•AB
∵AO=R，AB=2R
所以AE•AF=2R2．
点评：本题考查了圆周角定理的推论：直径所对的圆周角为90度以及三角形相似的判定与性质．
解答：
证明：连接BE，如图，∵AB为⊙O的直径
∴∠AEB=90°
∵AB⊥CD
∴∠AOF=90°
∴∠AOF=∠AEB=90°
又∠A=∠A
∴△AOF∽△AEB
∴AE•AF=AO•AB
∵AO=R，AB=2R
所以AE•AF=2R2．
点评：本题考查了圆周角定理的推论：直径所对的圆周角为90度以及三角形相似的判定与性质．
练习册系列答案
相关题目
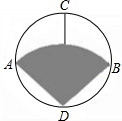某种商品的商标图案如图（图中的阴影部分），已知⊙O的直径AB⊥CD，且AB=8cm，弧AB是以D为圆心，DA为半径的弧，则商标图案的面积为
已知⊙O的直径AB=10，有一动点C从A点沿圆周顺时针向点B运动，若点D为弦AC所对弧的三等分点，过点D作DE⊥AB于E，直线AC交直线DB于G，点C、D都不与直径AB两端点重合，
如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=