题目内容
在△ABC中,∠BAC=120°,AB=AC=10 cm,一动点P从B向C以2cm/s的速度移动。问当P移动多少秒时,PA与腰垂直?(12分)
cm,一动点P从B向C以2cm/s的速度移动。问当P移动多少秒时,PA与腰垂直?(12分)
5秒或者10秒
解(1)设P点运动到如图所示位置时PA⊥AC

因为∠BAC=120° AB=AC
所以∠B=∠C=30°
因为PA⊥AC
所以∠PAC=90°
所以∠BAP=30°=∠B
所以PA=PB
设PA=PB=X
在PB△PAC中,∠C=30°
所以AP=
即PC=2x
根据勾股定理
PA2+AC2=PC2
即x2+(10 )2=2x2
)2=2x2
解得:x=10
即PA=PB=10cm
10÷2=5
当P移动5秒时,PA与腰AC垂直
(2)当P点继续移动到如图(2)所示位置时PA⊥AB

由(1)可知此时
PA=PC=10cm
BP=2PA=20cm
20÷2=10秒
即当P点移动10秒时,PA与腰AB垂直。解析:
本题要注意两种情况,即PA分别与两个腰垂直。
解(1)设P点运动到如图所示位置时PA⊥AC

因为∠BAC=120° AB=AC
所以∠B=∠C=30°
因为PA⊥AC
所以∠PAC=90°
所以∠BAP=30°=∠B
所以PA=PB
设PA=PB=X
在PB△PAC中,∠C=30°
所以AP=

即PC=2x
根据勾股定理
PA2+AC2=PC2
即x2+(10
 )2=2x2
)2=2x2解得:x=10
即PA=PB=10cm
10÷2=5
当P移动5秒时,PA与腰AC垂直
(2)当P点继续移动到如图(2)所示位置时PA⊥AB

由(1)可知此时
PA=PC=10cm
BP=2PA=20cm
20÷2=10秒
即当P点移动10秒时,PA与腰AB垂直。解析:
本题要注意两种情况,即PA分别与两个腰垂直。

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.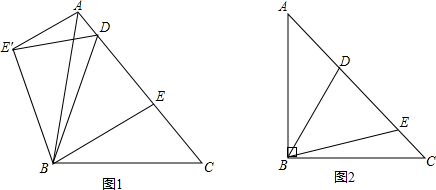
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.