题目内容
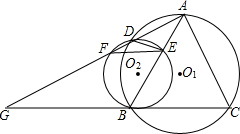已知，如图，△ABC内接于⊙O1，AB=AC，⊙O2与BC相切于点B，与AB相交于点E，与⊙O1相交于点D，直线AD交⊙O2于点F，交CB的延长线于点G．求证：（1）∠G=∠AFE；（2）AB•EB=DE•AG．
分析：（1）连接BD；若∠G=∠AFE成立，则EF必定和CG平行，那么一定有∠FEB=∠ABC；而在题中∠ABC=∠C，所以必须证明∠FEB=∠C，在这里可以以∠FDB为媒介；因为∠FEB和∠FDB为⊙O2中同弧所对圆周角相等，同时∠FDB又是⊙O1内接四边形的一个外角所以∠FDB=∠C，因此最终可证明结论成立．
（2）证AB•EB=DE•AG，即证
=
，而BE=BF可证，所以整个式子就又转化为
=
；而作为
来讲，由△ADE∽△ABF可得
=
，由EF∥CG可得
=
；由此可得出我们所要的结论．
（2）证AB•EB=DE•AG，即证
| DE |
| BE |
| AB |
| AG |
| DF |
| BF |
| AB |
| AG |
| AB |
| AG |
| DE |
| BF |
| AE |
| AF |
| AE |
| AF |
| AB |
| AG |
解答：
证明：（1）连接BD．
∵∠FEB=∠FDB，∠FDB=∠C，
∴∠FEB=∠C．
又∵AB=AC，
∴∠ABC=∠C．
∴∠FEB=∠ABC．
∴EF∥CG．
∴∠G=∠AFE．
（2）连接BF．
∵∠ADE=∠ABF，∠DAE=∠BAF，
∴△ADE∽△ABF．
∴
=
．
又∵EF∥CG，
∴
=
即
=
．
∵∠BEF=∠ABC，∠ABC=∠BFE，
∴∠BEF=∠BFE．
∴BE=BF．
∴
=
，即AB•EB=DE•AG．
证明：（1）连接BD．∵∠FEB=∠FDB，∠FDB=∠C，
∴∠FEB=∠C．
又∵AB=AC，
∴∠ABC=∠C．
∴∠FEB=∠ABC．
∴EF∥CG．
∴∠G=∠AFE．
（2）连接BF．
∵∠ADE=∠ABF，∠DAE=∠BAF，
∴△ADE∽△ABF．
∴
| DE |
| BF |
| AE |
| AF |
又∵EF∥CG，
∴
| AE |
| AF |
| AB |
| AG |
| DF |
| BF |
| AB |
| AG |
∵∠BEF=∠ABC，∠ABC=∠BFE，
∴∠BEF=∠BFE．
∴BE=BF．
∴
| DE |
| BE |
| AB |
| AG |
点评：此题主要考查的是在圆中相似三角形的判定和性质的应用，难易程度适中．
练习册系列答案
相关题目
17、已知，如图，△ABC中，∠BAC=90°，AD⊥BC于点D，BE平分∠ABC，交AD于点M，AN平分∠DAC，交BC于点N．
已知：如图，∠ABC、∠ACB 的平分线相交于点F，过F作DE∥BC于D，交AC 于E，且AB=6，AC=5，求三角形ADE的周长．
已知：如图，△ABC是等边三角形，点D在AB上，点E在AC的延长线上，且BD=CE，DE交BC于F，求证：BF=CF+CE．
已知：如图，△ABC中，AB=AC=10，BC=16，点D在BC上，DA⊥CA于A．
已知：如图，△ABC中，AD⊥BC，BD=DE，点E在AC的垂直平分线上．