Question

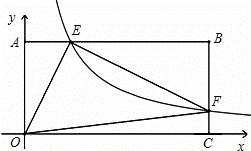
如图，将一矩形OABC放在直角坐标系中，O为坐标原点．点A在y轴正半轴上．点E是边AB上的一个动点（不与点A、B重合），过点E的反比例函数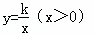的图象与边BC交于点F．

（1）若△OAE、△OCF的面积分别为S₁、S₂．且S₁+S₂=2，求k的值；

（2）若OA=2.0C=4．问当点E运动到什么位置时．四边形OAEF的面积最大．其最大值为多少？

Answer 1

解：（1）∵点E、F在函数y=（x＞0）的图象上，

∴设E（x₁，），F（x₂，），x₁＞0，x₂＞0，

∴S₁=，S₂=，

∵S₁+S₂=2，

∴=2，

∴k=2；

（2）∵四边形OABC为矩形，OA=2，OC=4，

设，，

∴BE=4﹣，BF=2﹣，

∴S_△BEF=﹣k+4，

∵S_△OCF=，S_矩形OABC=2×4=8，

∴S_{四边形OAEF}=S_矩形OABC﹣S_△BEF﹣S_△OCF=+4，

=﹣+5，

∴当k=4时，S_{四边形OAEF}=5，

∴AE=2．

当点E运动到AB的中点时，四边形OAEF的面积最大，最大值是5．