题目内容
如图所示，△ABC中，∠A=50°，点D，E分别在AB，AC上，则∠1+∠2的大小为 度．
【答案】分析：本题考查的是三角形内角和定理以及四边形内角和定理．
解答：解：∵∠A=50°?∠C+∠B=180°-∠A=130°．
又∵四边形ECBD内角和为360°，
∴∠1+∠2=360°-（∠C+∠B）=230°，
∴∠1+∠2=230°．
故填230．
点评：本题先利用三角形内角和定理求出∠C，∠B的度数，再利用四边形内角和求出∠1，∠2即可．
解答：解：∵∠A=50°?∠C+∠B=180°-∠A=130°．
又∵四边形ECBD内角和为360°，
∴∠1+∠2=360°-（∠C+∠B）=230°，
∴∠1+∠2=230°．
故填230．
点评：本题先利用三角形内角和定理求出∠C，∠B的度数，再利用四边形内角和求出∠1，∠2即可．
练习册系列答案
ABC考王全优卷系列答案
相关题目
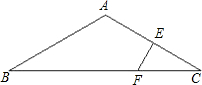如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=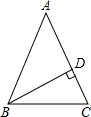
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．