题目内容
5.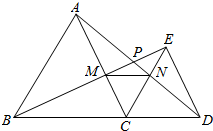 已知如图:△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②AN=BM;③∠APM=60°;④△CMN是等边三角形;⑤MN∥BD;⑥PC平分∠BPD,其中,正确的是①②③④⑤⑥(填写序号)
已知如图:△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②AN=BM;③∠APM=60°;④△CMN是等边三角形;⑤MN∥BD;⑥PC平分∠BPD,其中,正确的是①②③④⑤⑥(填写序号)
分析 ①根据等边三角形的性质得CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,则∠ACE=60°,利用“SAS”可判断△ACD≌△BCE,则AD=BE;
②由△ACD≌△BCE得到∠CAD=∠CBE,然后根据“ASA”判断△ACN≌△BCM,所以AN=BM;
③根据三角形内角和定理可得∠CAD+∠CDA=60°,而∠CAD=∠CBE,则∠CBE+∠CDA=60°,然后再利用三角形内角和定理即可得到∠BPD=120°,即可得到结论;
④由△ACN≌△BCM得到CN=BM,加上∠MCN=60°,则根据等边三角形的判定即可得到△CMN为等边三角形;
⑤由△CMN为等边三角形得到∠CMN=60°,所以∠CMN=∠BCM,于是根据平行线的判定即可得到MN∥BC;
⑥作CH⊥BE于H,CQ⊥AD于Q,如图,由△ACD≌△BCE得到CQ=CH,于是根据角平分线的判定定理即可得到CP平分∠BPD.
解答 证明:①∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACE=60°,
∴∠ACD=∠BCE=120°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE;
②∵△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACN和△BCM中,
$\left\{\begin{array}{l}{∠ACN=∠BCM}\\{CA=CB}\\{∠CAN=∠CBM}\end{array}\right.$,
∴△ACN≌△BCM(ASA),
∴AN=BM;
③∵∠CAD+∠CDA=60°,
而∠CAD=∠CBE,
∴∠CBE+∠CDA=60°,
∴∠BPD=120°,
∴∠APM=60°;
④∵△ACN≌△BCM,
∴CN=BM,
而∠MCN=60°,
∴△CMN为等边三角形;
⑤∵△CMN为等边三角形;
∴∠CMN=60°,
∴∠CMN=∠BCM,
∴MN∥BC;
⑥作CH⊥BE于H,CQ⊥AD于Q,如图,
∵△ACD≌△BCE,
∴CQ=CH,
∴CP平分∠BPD.
故答案为:①②③④⑤⑥.
点评 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.


若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为531,则开始输入的x值可能有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=2,DB=4,则$\frac{AE}{AC}$的值为( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=2,DB=4,则$\frac{AE}{AC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
| 年份 | 2008 | 2009 | 2010 | 1211 | 2012 |
| 产值/万元 | 80 | 90 | 110 | 130 | 155 |
| A. | 2009年 | B. | 2011年 | C. | 2010年 | D. | 2012年 |
 如图,AC=BC,点0为AB的中点,AC⊥BC,∠MON=45°,求证:CN+MN=AM.
如图,AC=BC,点0为AB的中点,AC⊥BC,∠MON=45°,求证:CN+MN=AM.