题目内容
15.某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要150a元.
分析 作BA边的高CD,设与BA的延长线交于点D,则∠DAC=30°,由AC=30m,即可求出CD=15m,然后根据三角形的面积公式即可推出△ABC的面积为150m2,最后根据每平方米的售价即可推出结果.
解答 解:如图,作BA边的高CD,设与BA的延长线交于点D,
∵∠BAC=150°,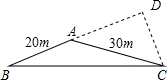
∴∠DAC=30°,
∵CD⊥BD,AC=30m,
∴CD=15m,
∵AB=20m,
∴S△ABC=$\frac{1}{2}$AB×CD=$\frac{1}{2}$×20×15=150m2,
∵每平方米售价a元,
∴购买这种草皮的价格为150a元.
故答案为:150a.
点评 本题主要考查三角形的面积公式,含30度角的直角三角形的性质,关键在于做出AB边上的高,根据相关的性质推出高CD的长度,正确的计算出△ABC的面积.

练习册系列答案
相关题目
6.正比例函数y=kx的图象与x轴的夹角为60°,且y的值随x的增大而减小,则该正比例函数的表达式为( )
| A. | y=-2x | B. | y=-$\sqrt{3}$x | C. | y=-$\frac{\sqrt{3}}{2}$x | D. | y=2x |
6.小明从一片树林的第m棵数起,一直数到第n棵(n>m),他数过的树的棵数是( )
| A. | m+n | B. | n-m | C. | n-m-1 | D. | n-m+1 |
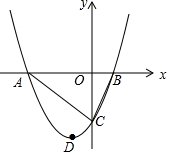 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴相交于点A(-3,0)和点B(1,0),与y轴相交于点C(0,-3),抛物线的顶点为点D,连接AC、BC.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴相交于点A(-3,0)和点B(1,0),与y轴相交于点C(0,-3),抛物线的顶点为点D,连接AC、BC. 如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF.若AE=4cm,则AG=2或6cm.
如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF.若AE=4cm,则AG=2或6cm. 小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息: 甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题:
甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题: