题目内容
点A(-1,0)B(4,0)C(0,2)是平面直角坐标系上的三点。
① 如图1先过A、B、C作△ABC,然后在在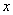 轴上方作一个正方形D1E1F1G1,
轴上方作一个正方形D1E1F1G1,
使D1E1在AB上, F1、G1分别在BC、AC上
② 如图2先过A、B、C作圆⊙M,然后在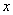 轴上方作一个正方形D2E2F2G2,
轴上方作一个正方形D2E2F2G2,
使D2E2在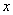 轴上 ,F2、G2在圆上
轴上 ,F2、G2在圆上
③ 如图3先过A、B、C作抛物线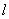 ,然后在
,然后在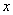 轴上方作一个正方形D3E3F3G3,
轴上方作一个正方形D3E3F3G3,
使D3E3在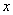 轴上, F3、G3在抛物线上
轴上, F3、G3在抛物线上
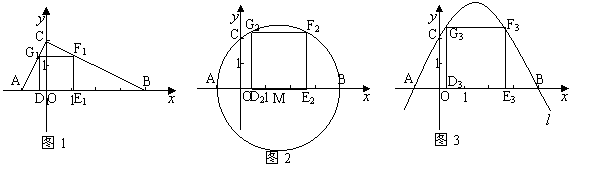
请比较 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面积大小
 |
解:图1 设正方形的边长为
由△CG1F1∽△CAB 得 
∴ ∴
∴
图2 设正方形的边长为
∵A(-1,0)B(4,0)C(0,2)
∴
∴∠ACB=90° ∴AB是圆M的直径
过M作MN⊥G2F2 由垂径定理得
解得 即
即
图3 设正方形的边长为
由A(-1,0)B(4,0)C(0,2)得抛物线为
由轴对称性可知 F3( ,
, ) 代入得
) 代入得
解得 ∴
∴
∵
∴ <
< <
<

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ° C.90° D.180°
° C.90° D.180° 中,
中, ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持 .连接DE、DF、EF.在此运动变化的过程中,下列结论:①
.连接DE、DF、EF.在此运动变化的过程中,下列结论:① 是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是( )
是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是( )


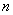 是正整数,则奇数可以用代数式
是正整数,则奇数可以用代数式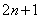 来表示.
来表示. ;
; B.
B. C.
C. D.
D.
 ABCD中,∠B的平分线BE交AD于E,AE=10,ED=4,那么
ABCD中,∠B的平分线BE交AD于E,AE=10,ED=4,那么
 ,则
,则 。
。  ,当k>0时,y随x的增大而减少。
,当k>0时,y随x的增大而减少。  为线段
为线段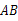 的中点,
的中点, 与
与 交于点
交于点 ,∠
,∠ ∠
∠ ∠
∠ 且
且 交
交 于点F,
于点F, 交
交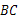 于
于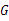 .写出图中两对相似三角形,并证明其中的一对.
.写出图中两对相似三角形,并证明其中的一对.