题目内容
已知a+b=8，且a2-b2=48，则式子a-3b的值是________
4
分析：由已知得（a+b）（a-b）=48，把a+b=8代入得a-b=6，由此可求a、b的值，再求式子a-3b的值．
解答：由a2-b2=48得（a+b）（a-b）=48，
把a+b=8代入得a-b=6，
解方程组
，得
∴a-3b=7-3×1=4．
故本题答案为4．
点评：本题考查了平方差公式的实际运用，关键是能将已知条件因式分解，整体代入得出方程组求解．
分析：由已知得（a+b）（a-b）=48，把a+b=8代入得a-b=6，由此可求a、b的值，再求式子a-3b的值．
解答：由a2-b2=48得（a+b）（a-b）=48，
把a+b=8代入得a-b=6，
解方程组
，得∴a-3b=7-3×1=4．
故本题答案为4．
点评：本题考查了平方差公式的实际运用，关键是能将已知条件因式分解，整体代入得出方程组求解．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
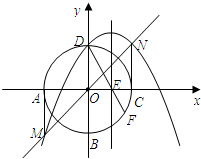C、D四点．过点A和点C分别作⊙O的切线MA、NC，它们分别与直线y=x交于点M、N，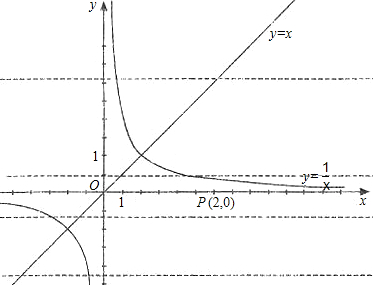
已知直线l1∥l2，且 l3、l4和l1、l2分别交于A、B、C、D四点，点P在直线AB上运动．设∠ADP=∠1，∠DPC=∠2，∠BCP=∠3．