题目内容
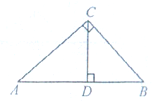
(2011?常州)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=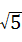 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A、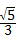 B、
B、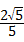
C、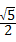 D、
D、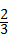
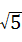 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A、
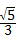 B、
B、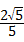
C、
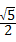 D、
D、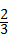
A
分析:在直角△ABC中,根据勾股定理即可求得AB,而∠B=∠ACD,即可把求sin∠ACD转化为求sinB.
解答:解:在直角△ABC中,根据勾股定理可得:AB= =
= =3.
=3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD.
∴sin∠ACD=sin∠B= =
= ,
,
故选A.
解答:解:在直角△ABC中,根据勾股定理可得:AB=
 =
= =3.
=3.∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD.
∴sin∠ACD=sin∠B=
 =
= ,
,故选A.

练习册系列答案
相关题目
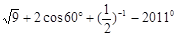 .
. ∥AB,F是
∥AB,F是 »1.414,
»1.414, »1.732,
»1.732, »2.449,供选用)
»2.449,供选用)
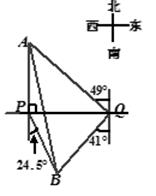

 A的值等于
A的值等于