��Ŀ����
��2010•������һģ����ͼ��������y= x2+mx+n��x����A��B���㣬ֱ��y=kx+b������A�������������ߵĶԳ��ύ�ڵ�M��1��2�����ҵ�M�������ߵĶ���N����x��Գƣ�
x2+mx+n��x����A��B���㣬ֱ��y=kx+b������A�������������ߵĶԳ��ύ�ڵ�M��1��2�����ҵ�M�������ߵĶ���N����x��Գƣ���1�������������ߵĺ�����ϵʽ��
��2�������е���������ֱ�ߵ���һ����ΪC����֪PΪ�߶�AC��һ�㣨�����˵㣩������P��PQ��x�ᣬ���������ڵ�Q����֤������PΪAC���е�ʱ���߶�PQ�ij�ȡ�����ֵ�������PQ�����ֵ��
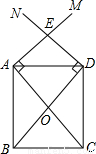
��3����D��EΪֱ��AC�ϵ����㣨����A��C�غϣ�����D��E����࣬DE=2
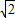 ������D��DF��x�ύ�������ڵ�F������E��EG��x�ύ�������ڵ�G���ʣ��Ƿ���������ĵ�D��ʹ����D��E��F��GΪ������ı���Ϊƽ���ı��Σ������ڣ���������з��������ĵ�D�����ꣻ�������ڣ���˵�����ɣ�
������D��DF��x�ύ�������ڵ�F������E��EG��x�ύ�������ڵ�G���ʣ��Ƿ���������ĵ�D��ʹ����D��E��F��GΪ������ı���Ϊƽ���ı��Σ������ڣ���������з��������ĵ�D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���������1�����ڵ�M�������߶������x��Գƣ����ɵõ���N�����꣬������ʾ���������ߵĶ�������ʽ��������ʽ��
��2�����ݣ�1�����������ߵĽ���ʽ���ɵõ���A�����꣬���������ֱ��AC�Ľ���ʽ�������P�ĺ����꣬����ֱ��AC�������ߵĽ���ʽ�����ɵõ�P��Q�������꣬�Ӷ��õ�����PQ�ij���P�������ĺ�����ϵʽ���������ú��������ʼ������PQ�����ֵ����Ӧ��P�����꣬Ȼ���жϴ�ʱ��P���Ƿ�ΪAC���е㼴�ɣ�
��3����ֱ��AC��б�ʿɵá�CAB=45°�����D��E�ĺ������Ϊ2���������D�ĺ����꣬���ɵõ���E�ĺ����꣬�����ɲ��գ�2���ķ������DF��EG�ij�������D��E��F��GΪ������ı���Ϊƽ���ı��Σ���ô��������DE=FG���ɴ˿���õ�D�����꣮��Ҫע����ǣ��ڱ�ʾDE��FG�ij�ʱ��Ҫ������������ǣ�
�ٵ�D���߶�CA���ӳ����ϣ�E���߶�AC�ϣ���D��E�����߶�AC�ϣ��۵�E���߶�AC���ӳ����ϣ�D���߶�AC�ϣ�
����⣺��1��������֪�������߶���N������Ϊ��1��-2������1�֣�
���亯����ϵʽΪy= ��x-1��2-2=
��x-1��2-2= x2-x-
x2-x- ����3�֣�
����3�֣�
��2���� x2-x-
x2-x- =0
=0
��x=-1��3����A��-1��0����B��3��0����
��A��-1��0����M��1��2���ɵ�ֱ��AC�ĺ�����ϵʽΪy=x+1����4�֣�
��P��t��t+1������Q��������t�� t2-t-
t2-t- ������5�֣�
������5�֣�
��PQ=��t+1��-�� t2-t-
t2-t- ��=-
��=- t2+2t+
t2+2t+ =-
=- ��t-2��2+
��t-2��2+ ����6�֣�
����6�֣�
��a=- ��0
��0
�൱t=2ʱ��PQ�����ֵΪ ��
��
��P���˶���AC���е�ʱ��PQ�������ֵΪ ����7�֣�
����7�֣�
��3����ֱ��AC�ĺ�����ϵʽΪy=x+1��֪����CAB=45°����D��E�ĺ������Ϊ2��
���D��x��x+1����E��x+2��x+3������F��x�� x2-x-
x2-x- ����G��x+2��
����G��x+2�� x2+x-
x2+x- ����
����
����DF��EG������D��E��F��GΪ������ı���Ϊƽ���ı��Σ���DF=EG��
�ٵ���D���߶�CA���ӳ����ϣ���E���߶�AC��ʱ��
DF= x2-x-
x2-x- -��x+1��=
-��x+1��= x2-2x-
x2-2x- ��EG=x+3-��
��EG=x+3-�� x2+x-
x2+x- ��=-
��=- x2+
x2+ ��
��
����DF=EG���� x2-2x-
x2-2x- =-
=- x2+
x2+ ��
��
���x=1±2 ��
��
����x��0����D��1-2 ��2-2
��2-2 ����
����
�ڵ���D��E�����߶�AC��ʱ��
DF=- x2+2x+
x2+2x+ ��EG=-
��EG=- x2+
x2+ ��
��
ͬ�ٿɵã�- x2+2x+
x2+2x+ =-
=- x2+
x2+ ��
��
���x=1��
��D��1��2����
�۵���D���߶�AC�ϣ�E�����߶�AC���ӳ�����ʱ��
DF= x2-x-
x2-x- -��x+1��=
-��x+1��= x2-2x-
x2-2x- ��EG=x+3-��
��EG=x+3-�� x2+x-
x2+x- ��=-
��=- x2+
x2+ ��
��
����DF=EG���� x2-2x-
x2-2x- =-
=- x2+
x2+ ��
��
���x=1±2 ��
��
����x��0����D��1+2 ��2+2
��2+2 ����
����
���������ĵ㹲��3�����ֱ�ΪD1��1��2����D2��1-2 ��2-2
��2-2 ����D3��1+2
����D3��1+2 ��2+2
��2+2 ������11�֣�
������11�֣�
���ڣ�3��С��ó�1��ã�2�֣���2��ã�3�֣���3���4�֣�
������������Ҫ�����˶��κ�������ʽ��ȷ��������ͼ������������κ�����ֵ��Ӧ�á�ƽ���ı��ε��ж������ʵ�֪ʶ��ͬʱ�����˷������۵���ѧ˼�룬�ѶȽϴ�
��2�����ݣ�1�����������ߵĽ���ʽ���ɵõ���A�����꣬���������ֱ��AC�Ľ���ʽ�������P�ĺ����꣬����ֱ��AC�������ߵĽ���ʽ�����ɵõ�P��Q�������꣬�Ӷ��õ�����PQ�ij���P�������ĺ�����ϵʽ���������ú��������ʼ������PQ�����ֵ����Ӧ��P�����꣬Ȼ���жϴ�ʱ��P���Ƿ�ΪAC���е㼴�ɣ�
��3����ֱ��AC��б�ʿɵá�CAB=45°�����D��E�ĺ������Ϊ2���������D�ĺ����꣬���ɵõ���E�ĺ����꣬�����ɲ��գ�2���ķ������DF��EG�ij�������D��E��F��GΪ������ı���Ϊƽ���ı��Σ���ô��������DE=FG���ɴ˿���õ�D�����꣮��Ҫע����ǣ��ڱ�ʾDE��FG�ij�ʱ��Ҫ������������ǣ�
�ٵ�D���߶�CA���ӳ����ϣ�E���߶�AC�ϣ���D��E�����߶�AC�ϣ��۵�E���߶�AC���ӳ����ϣ�D���߶�AC�ϣ�
����⣺��1��������֪�������߶���N������Ϊ��1��-2������1�֣�
���亯����ϵʽΪy=
 ��x-1��2-2=
��x-1��2-2= x2-x-
x2-x- ����3�֣�
����3�֣���2����
 x2-x-
x2-x- =0
=0��x=-1��3����A��-1��0����B��3��0����
��A��-1��0����M��1��2���ɵ�ֱ��AC�ĺ�����ϵʽΪy=x+1����4�֣�
��P��t��t+1������Q��������t��
 t2-t-
t2-t- ������5�֣�
������5�֣���PQ=��t+1��-��
 t2-t-
t2-t- ��=-
��=- t2+2t+
t2+2t+ =-
=- ��t-2��2+
��t-2��2+ ����6�֣�
����6�֣���a=-
 ��0
��0 �൱t=2ʱ��PQ�����ֵΪ
 ��
����P���˶���AC���е�ʱ��PQ�������ֵΪ
 ����7�֣�
����7�֣���3����ֱ��AC�ĺ�����ϵʽΪy=x+1��֪����CAB=45°����D��E�ĺ������Ϊ2��
���D��x��x+1����E��x+2��x+3������F��x��
 x2-x-
x2-x- ����G��x+2��
����G��x+2�� x2+x-
x2+x- ����
��������DF��EG������D��E��F��GΪ������ı���Ϊƽ���ı��Σ���DF=EG��
�ٵ���D���߶�CA���ӳ����ϣ���E���߶�AC��ʱ��
DF=
 x2-x-
x2-x- -��x+1��=
-��x+1��= x2-2x-
x2-2x- ��EG=x+3-��
��EG=x+3-�� x2+x-
x2+x- ��=-
��=- x2+
x2+ ��
������DF=EG����
 x2-2x-
x2-2x- =-
=- x2+
x2+ ��
�����x=1±2
 ��
������x��0����D��1-2
 ��2-2
��2-2 ����
�����ڵ���D��E�����߶�AC��ʱ��
DF=-
 x2+2x+
x2+2x+ ��EG=-
��EG=- x2+
x2+ ��
��ͬ�ٿɵã�-
 x2+2x+
x2+2x+ =-
=- x2+
x2+ ��
�����x=1��
��D��1��2����
�۵���D���߶�AC�ϣ�E�����߶�AC���ӳ�����ʱ��
DF=
 x2-x-
x2-x- -��x+1��=
-��x+1��= x2-2x-
x2-2x- ��EG=x+3-��
��EG=x+3-�� x2+x-
x2+x- ��=-
��=- x2+
x2+ ��
������DF=EG����
 x2-2x-
x2-2x- =-
=- x2+
x2+ ��
�����x=1±2
 ��
������x��0����D��1+2
 ��2+2
��2+2 ����
�������������ĵ㹲��3�����ֱ�ΪD1��1��2����D2��1-2
 ��2-2
��2-2 ����D3��1+2
����D3��1+2 ��2+2
��2+2 ������11�֣�
������11�֣����ڣ�3��С��ó�1��ã�2�֣���2��ã�3�֣���3���4�֣�
������������Ҫ�����˶��κ�������ʽ��ȷ��������ͼ������������κ�����ֵ��Ӧ�á�ƽ���ı��ε��ж������ʵ�֪ʶ��ͬʱ�����˷������۵���ѧ˼�룬�ѶȽϴ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ