题目内容
5、已知在梯形ABCD中，AD∥BC，AC⊥BD，判断AD+BC与AB+CD的大小关系：AD+BC
＜
AB+CD．分析：要判断AD+BC与AB+CD的大小关系，通常思路是借助三角形三边关系来解答，然而这些线段并不在同一个三角形中，所以要设法利用辅助线来达到上述目的．
解答：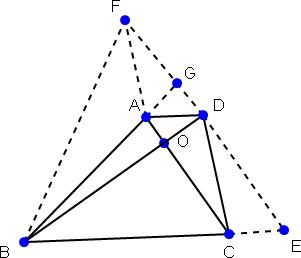
解：如图；
过D作DE∥AC，交BC的延长线于E；
过A作AF∥CD，交ED的延长线于F；
延长BA交DF于G，连接BF；
由于BD⊥AC，则BD⊥EF；
由勾股定理得：
BE2=BD2+DE2，BF2=BD2+DF2；
由于AC∥EF，AD∥CE，AF∥CD，可得：
四边形ACED、四边形AFDC都是平行四边形，则有：
AF=DC，DF=AC=DE，AD=CE，BE=AD+BC；
∴BF2=BD2+DF2=BD2+DE2=BE2，即BF=BE=AD+BC；
在△ABF中，AB+AF＞BF，即AB+CD＞BF；
而BF=AD+BC，即AD+BC＜AB+CD．
故答案为：＜．
解：如图；过D作DE∥AC，交BC的延长线于E；
过A作AF∥CD，交ED的延长线于F；
延长BA交DF于G，连接BF；
由于BD⊥AC，则BD⊥EF；
由勾股定理得：
BE2=BD2+DE2，BF2=BD2+DF2；
由于AC∥EF，AD∥CE，AF∥CD，可得：
四边形ACED、四边形AFDC都是平行四边形，则有：
AF=DC，DF=AC=DE，AD=CE，BE=AD+BC；
∴BF2=BD2+DF2=BD2+DE2=BE2，即BF=BE=AD+BC；
在△ABF中，AB+AF＞BF，即AB+CD＞BF；
而BF=AD+BC，即AD+BC＜AB+CD．
故答案为：＜．
点评：此题的难点在于将所求的线段转换到同一个三角形中，而正确的做出辅助线是顺利解题的前提；题目综合了梯形、勾股定理、平行四边形、三角形的三边关系等重要知识点，难度较大．
练习册系列答案
相关题目
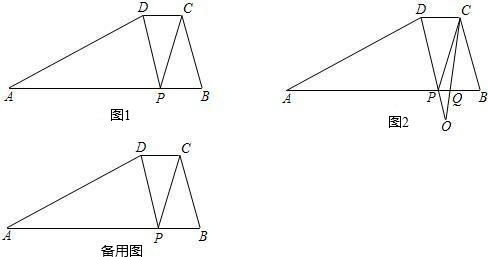
9、如图，已知在梯形ABCD中，AD∥BC，AB=DC，对角线AC和BD相交于点O，E是BC边上一个动点（E点不与B、C两点重合），EF∥BD交AC于点F，EG∥AC交BD于点G．
；