Question

已知：如图，两圆相交于A，B两点，过A点的割线分别交两圆于D，F点，过B点的割线分别交两圆于H，E点．求证：HD∥EF．

Answer 1

证明：连接AB，
∵∠A与∠BHD是对的圆周角，
∴∠A=∠BHD，
∵∠A与∠BEF是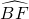对圆周角，
∴∠A=∠BEF，
∴∠BHD=∠BEF，
∴HD∥EF．
分析：首先连接AB，根据在同圆或等圆中，同弧或等弧所对的圆周角相等，即可得∠A=∠BHD，∠A=∠BEF，然后根据同位角相等，两直线平行，证得HD∥EF．
点评：此题考查了圆周角定理与平行线的判定．此题难度不大，解题的关键是准确作出辅助线，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等定理的应用．