题目内容
顺次连结等腰梯形各边中点所得的四边形一定是
- A.等腰梯形
- B.矩形
- C.菱形
- D.正方形
C
分析:因为等腰梯形的对角线相等,根据三角形中位线定理,所得四边形的各边都相等,所以判定为菱形.
解答: 解:如图所示.
解:如图所示.
根据三角形中位线定理,EF=GH= BD;FG=EH=
BD;FG=EH= AC.
AC.
∵ABCD为等腰梯形,∴AC=BD.
∴EF=GH=FG=EH.
∴EFGH为菱形.
故选C.
分析:因为等腰梯形的对角线相等,根据三角形中位线定理,所得四边形的各边都相等,所以判定为菱形.
解答:
 解:如图所示.
解:如图所示.根据三角形中位线定理,EF=GH=
 BD;FG=EH=
BD;FG=EH= AC.
AC.∵ABCD为等腰梯形,∴AC=BD.
∴EF=GH=FG=EH.
∴EFGH为菱形.
故选C.

练习册系列答案
相关题目
顺次连结等腰梯形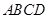 各边中点,所得的四边形一定是( )
各边中点,所得的四边形一定是( )
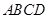 各边中点,所得的四边形一定是( )
各边中点,所得的四边形一定是( )| A.等腰梯形 | B.菱形 | C.矩形 | D.平行四边形 |
 各边中点,所得的四边形一定是( )
各边中点,所得的四边形一定是( )